Questo post prende il titolo, naturalmente, dall’Inferno di Dante ed è la traduzione della versione inglese dell’articolo pubblicato su moonphotoshop.com qualche giorno fa. Il suo scopo è quello di discutere un aspetto del metodo Lab ben noto ma probabilmente poco compreso in profondità.
Alcune domande sono più utili di altre quando è necessario verificare se un certo concetto è stato assimilato. Nei miei seminari e nelle classi una delle domande fondamentali è questa: “quanti primari cromatici ha il metodo Lab?” Una maggioranza significativa di persone risponde: quattro. Pensano – verde, magenta, blu, giallo. La risposta però è sbagliata: sono due. Verde-magenta e blu-giallo, per essere chiari.

È difficile immaginare un colore con due lati, e anche di più quando i due lati vengono definiti “opponenti”. In RGB, ad esempio, abbiamo il rosso, il verde e il blu, qualsiasi cosa questi termini significhino (il vero colore dipende dalle cromaticità). Sono diversi, ma non si parla mai di opposizione. Da fisico, credo che un semplice modello possa spingersi più in là delle equazioni quando è necessario esporre i concetti essenziali, e ne ho utilizzati diversi per spiegare la complessa idea dei colori che vivono appaiati. Uno dei modelli più ovvi è quello della bilancia a piatti: nel momento in cui accettiamo che i due canali cromatici di Lab (“a” e “b”) misurano la tendenza di un colore verso il verde o verso il magenta (a), oppure verso il blu o il giallo (b) e definiscono la neutralità come nessuna tendenza verso alcun colore, una bilancia è adatta a rappresentare la situazione. Di fatto, è utile anche perché ci permettere di visualizzare facilmente la strana proprietà dei canali a e b di assumere valori negativi o positivi, a differenza di ciò che accade con i canali RGB o CMYK. Se scende il piatto di sinistra, il numero è negativo; se scende quello di destra, è positivo.
C’è però un problema subdolo in questo modello: entrambi i piatti sono sempre visibili. Questo non è ciò che accade in Lab: se, per fare un esempio, un colore tende al magenta nel canale a (a > 0), la componente verde è assente. Non è possibile avere a > 0 e a < 0 allo stesso tempo; ovvero, non si possono vedere entrambi i piatti in una sola volta. Avanti un altro modello, dunque: il mio modo preferito per spiegare il funzionamento dei canali a e b si basa ora su un concetto ancora più semplice di quello della bilancia. Ovvero, una moneta.
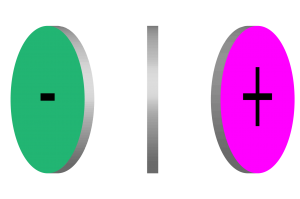
Potete verificare questo modello in maniera semplicissima: prendete la prima moneta che trovate e guardatela. Potete provarci finché volete, ma non riuscirete mai a vederne entrambe le facce. Al massimo riuscirete a guardare direttamente il bordo, il che significa che non state vedendo alcuna faccia. In qualsiasi modo giriate la moneta, potete soltanto vedere una sola faccia o nessuna faccia. La figura si spiega da sé, credo. Questa moneta rappresenta il canale a, e il canale b sarebbe identico, con il blu al posto del verde e il giallo al posto del magenta. Una delle facce è verde; l’altra faccia è magenta; il bordo non è né verde né magenta. Inoltre, più ruotate la moneta attorno al suo asse, più colore vedete, e questo corrisponde in qualche modo alla saturazione che cresce al crescere dei valori numerici. Ho aggiunto un segno meno e un segno più per ricordare che i colori freddi (verde, blu) sono espressi da numeri negativi mentre quelli caldi (magenta, giallo) vivono nel regno dei numeri positivi.
Questo modello rende anche conto del fatto che non è possibile passare da un colore al suo opponente senza attraversare prima la neutralità: se state osservando il lato verde della moneta dovete per forza ruotarla per vedere quello magenta; e per fare questo a un certo punto dovete necessariamente trovarvi davanti il bordo.
Un’osservazione finale. Esiste la verità scientifica ed esistono dei modelli suggestivi. I modelli a volte possono essere stirati al punto di invadere il campo della filosofia piuttosto che quello della scienza, e il colore è certamente uno dei campi in cui questa tentazione è forte. È un dato di fatto che più si pensa al colore, più dualistica la mente diventa: il contrasto simultaneo, ad esempio, viene facilmente considerato un aspetto fondamentale della percezione – non solo nel campo del colore. Pensiamo ad esempio alla temperatura: cosa significano parole come “freddo” e “caldo”? L’acqua può essere percepita come fredda o calda in funzione di vari fattori, incluso il fatto che le vostre mani siano state immerse in acqua più calda o più fredda fino a pochi secondi prima. Il fatto è che la temperatura, come fenomeno fisico, non è caratterizzabile come “calda” o “fredda”: è semplicemente connessa al moto molecolare, e misura una certa forma di energia disponibile nella materia. La nostra sensazione di “caldo” o “freddo” dipende da una quantità di condizioni che non sono oggettive come potremmo pensare, e il fenomeno è completamente legato alla nostra percezione – qualcosa che diamo per scontato ma che è, in realtà, un animale assai complesso e spesso in grado di confonderci.
Nella mia mente, e indipendentemente dal fatto che questo rispetti le regole sceintifiche o meno, trovo facile e affascinante pensare ai colori opponenti come a un unico colore che si manifesta in un certo modo a seconda della sua posizione rispetto a qualcosa che chiamiamo “neutralità”, che è un concetto evanescente come molti altri. Anche senza considerare condizioni temporanee e soggettive, percepiamo l’acqua come “fredda” o “calda” soprattutto in relazione alla nostra temperatura corporea: qualsiasi cosa abbia una temperatura significativamente più elevata di noi stessi ci sembrerà “calda”; se invece scendiamo più in basso, ecco arrivare il “freddo”. Ma la temperatura è la temperatura e, in Lab, il canale a è il canale a. La mia pelle non tende al magenta: è, semmai, più tendente al magenta di quanto non tenda al verde, e se affermo che ha una “componente magenta”, o che deve essere “positiva nel canale a” è soltanto perché uso un’espressione sintetica per semplificare le cose.
È anche interessante considerare che il terzo incomodo in questo gioco, il canale L, non è così diverso a ben guardare. La chiarezza è nulla quando il suo valore è pari a 0, e massima quando è pari a 100. Un valore pari a 50, che nuovamente se ne sta seduto a metà della scala, definisce un punto di equilibrio in cui la chiarezza ha un’eguale tendenza verso 0 o verso 100. Infatti il grigio 50% in Lab è definito come 50L0a0b. Potremmo affermare che questo valore centrale di L si comporta in maniera simile allo 0 in a e in b? Non sono “nero” e “bianco” colori opponenti di diritto, anche se acromatici? Ne parleremo più approfonditamente, un giorno.
Giratela come volete, come se fosse una moneta: l’idea di due entità opponenti che sono soltanto apparentemente tali, perché in realtà sono Una cosa sola, è affascinante. Il titolo di questo articolo pertanto mi sembra adatto: la formula è retorica, vi sento obiettare; ma serve un amore più che normale per diventare inseparabili. L’amore normale può essere disperso dal più lieve dei venti; ma se cercate di separare qualcosa di profondamente connesso come l’unità degli opposti, il risultato è: fail. Perseverate, e tutto ciò che vi rimarrà sarà un sistema completamente sfasciato che non vale nulla. Posso tranquillamente immaginare il verde dire al magenta: “Non posso più oppormi a te – è per te che sto lottando”. Sto rubando questa frase agli U2 e alla loro canzone Ordinary Love, che sospetto abbia a che fare con il colore (e con le nostre vite) più di quanto vorremmo ammettere. Provate a pensare a questa idea, anche voi, e potrebbero aprirvisi nuovi mondi.
Come forse immaginate, non ho il minimo interesse nell’amore normale, ma sono profondamente attratto dall’unità, e dal dualismo che genera. Il lato negativo di questo è che potreste essere condannati a leggere altri post di questo genere in futuro, e non sono sicuro che questo sia il modo migliore di preservare la vostra salute mentale… 😉
Il mio migliore augurio: siate opponenti!
MO


Grande… è disarmante come riesci a mettere filosofia e cuore in concetti fisici e prettamente matematici ai più.
E’ quello che rende le tue argomentazioni e le tue lezioni così interessanti ed indimenticabili: per i contenuti sicuramente, ma anche perchè quello che dici e scrivi è sotto i nostri occhi ogni giorno e tutto il giorno. Si riesce ad apprezzarne la natura e ad analizzarlo analiticamente per controllarlo in ambito creativo.
Se tutto questo significa perdere la sanità mentale, va benissimo, evviva la follia…
Andrea
è sempre un piacere leggere i tuoi articoli…
Anche per un analfabeta del “colore” come me.
tnks.
buona giornata.
Si dice sempre che il contenuto è più importante della forma: vero. Ma è anche vero che la forma può rafforzare il contenuto…e meno male. Per questo anche chi ha ben presente i concetti espressi da Marco, non può esimersi da continuare a leggere una riga dopo l’altra fino a giungere alla fine.
Grazie
Finirò per scoprire che la ruota dei colori e l’Enso sono parenti?
Articolo veramente ben scritto e strutturato come al tuo solito! Complimenti Marco
Grazie mille, Cosimo!
Semplicemente splendido: accetto la condanna!
Grazie Sergio!