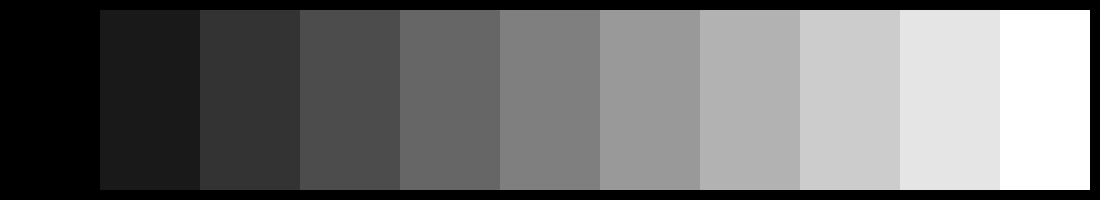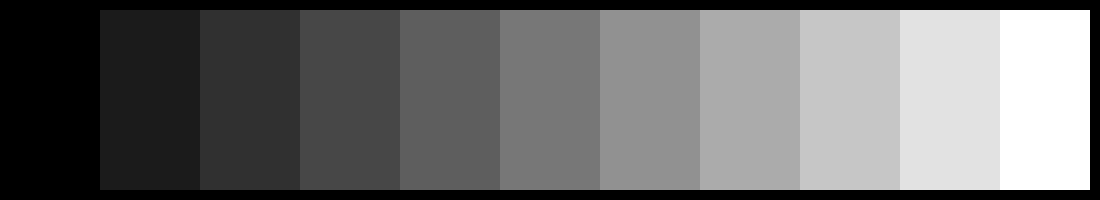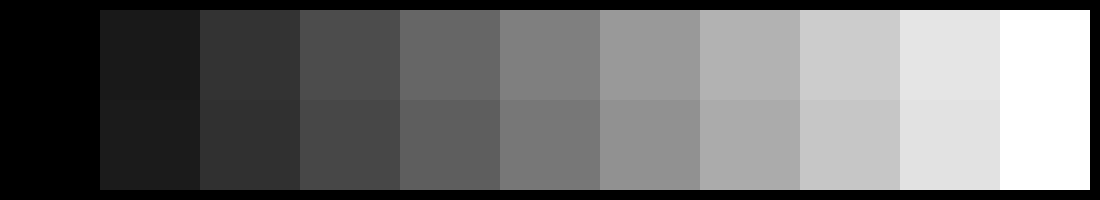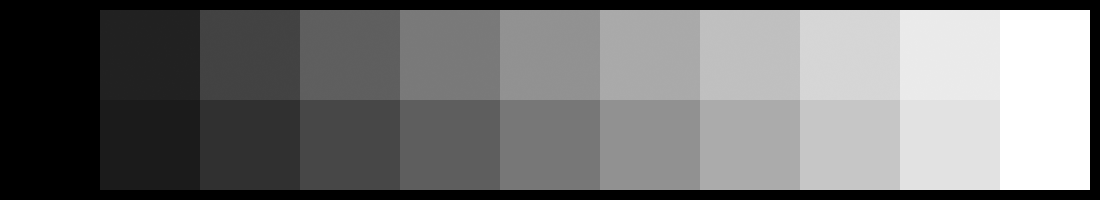Ha senso parlare della distanza tra due colori? Certamente sì, ma non è così semplice. Questo articolo vuole introdurre alcuni concetti di base che possono essere utili per capire quanto un certo colore differisca da un campione dato. Il risultato è un parametro ben noto, il DeltaE, che può essere di grande aiuto ma non dice tutto.
Cos’è la distanza?
I matematici sono assai precisi nelle definizioni. Abbiamo parlato molte volte di spazi colore, ma un matematico all’oscuro della loro esistenza certamente chiederebbe: “uno spazio colore è anche uno spazio metrico?”
Non allarmatevi, il concetto di base è semplice. Uno spazio metrico è definito come un insieme di punti nel quale è definita una distanza, detta anche metrica. Per maggiore precisione, è definita una funzione distanza che permette di misurare la distanza tra due punti appartenenti a quello spazio.
Utilizziamo spazi metrici nella vita reale senza quasi rendercene conto, ogni giorno. Li abbiamo studiati a scuola nel momento in cui abbiamo definito una scala su una linea retta, o abbiamo affrontato il piano cartesiano, o ci siamo spinti fino allo spazio tridimensionale – quello che di solito viene rappresentato per mezzo di tre assi cartesiani denominati x, y, z.
Lo spazio geometrico di Euclide
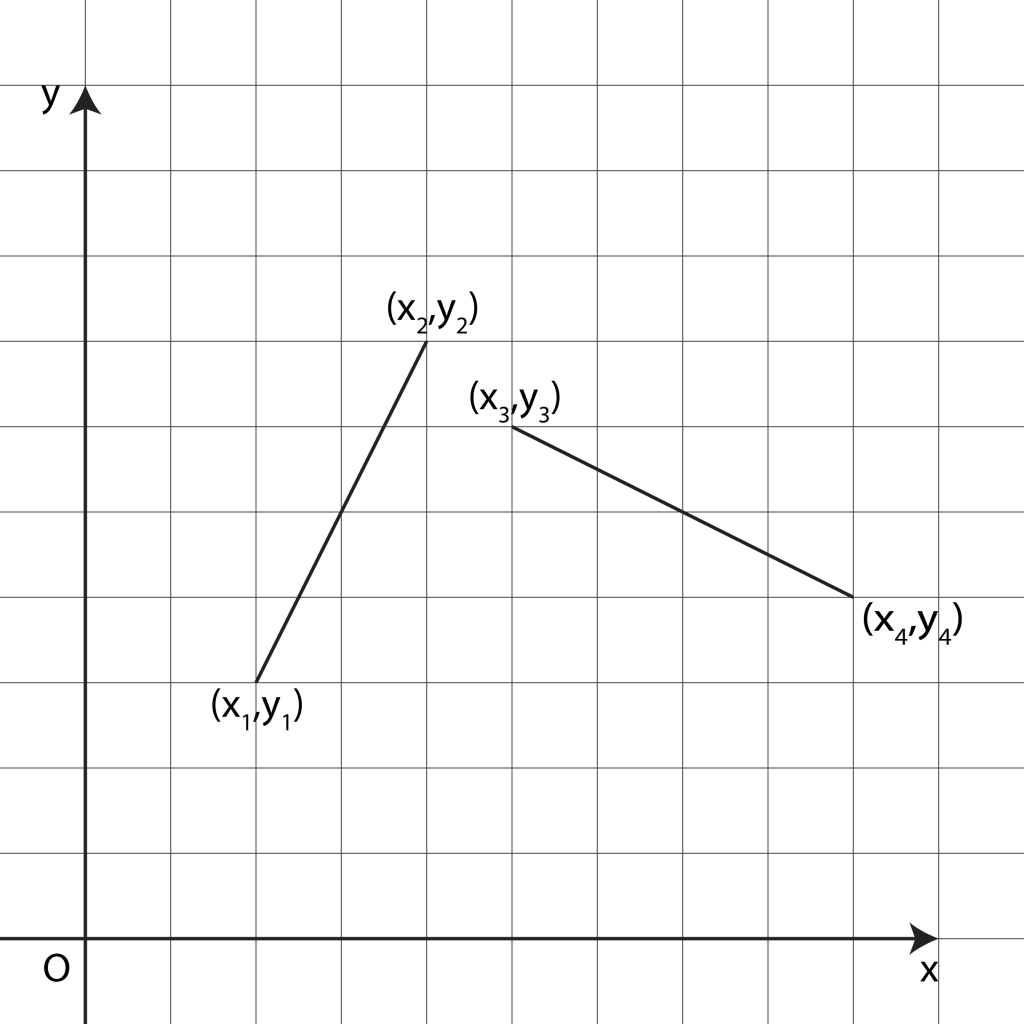
Se abbiamo due assi x, y sui quali definiamo un’unità di misura e un’origine, otteniamo uno spazio euclideo a due dimensioni. Il termine “euclideo” indica che in esso vale la geometria basata sui postulati di Euclide.
Il segmento più a sinistra ha come estremi due punti caratterizzati da coordinate ![]() e
e ![]() . Nel caso specifico, se consideriamo che i due assi siano suddivisi in unità e che l’origine O corrisponda con
. Nel caso specifico, se consideriamo che i due assi siano suddivisi in unità e che l’origine O corrisponda con ![]() , i due punti saranno rispettivamente
, i due punti saranno rispettivamente ![]() e
e ![]() : basta contare i quadretti per rendersene conto.
: basta contare i quadretti per rendersene conto.
Dal momento che abbiamo a che fare con uno spazio euclideo, possiamo definire la distanza tra i due punti come segue:
(1) ![]()
Sembra molto complicato, ma si tratta del vecchio e fedele teorema di Pitagora espresso in forma algebrica. Se ai simboli sostituiamo i numeri, calcolare la distanza dei due punti in esame diventa molto semplice:
(2) ![]()
Se volete, potete provare che anche l’altro segmento ha la stessa lunghezza: lo s’intuisce dal fatto che pur essendo diverso attraversa lo stesso numero di quadretti, ma è facile dimostrarlo anche algebricamente. A monte di tutto, però, c’è un’ipotesi fondamentale che presto discuteremo: che la scala che definisce i quadretti sia lineare.
Se avessimo a che fare con tre dimensioni invece che con due, non cambierebbe molto: i punti sarebbero espressi da terne del tipo ![]() e
e ![]() e la distanza diventerebbe:
e la distanza diventerebbe:
(3) ![]()
Dovrebbe risultare ovvio che la distanza può assumere il valore 0 solo se imponiamo condizioni precise: ![]() ,
, ![]() e
e ![]() . Le tre condizioni devono valere contemporaneamente. Questo è un modo sofisticato per affermare una cosa evidente: se due punti hanno distanza pari a zero, i due punti coincidono. Ovvero, hanno le stesse coordinate. Ovvero, per dirla terra terra, sono in pratica lo stesso punto.
. Le tre condizioni devono valere contemporaneamente. Questo è un modo sofisticato per affermare una cosa evidente: se due punti hanno distanza pari a zero, i due punti coincidono. Ovvero, hanno le stesse coordinate. Ovvero, per dirla terra terra, sono in pratica lo stesso punto.
x, y, z sono ciò che vogliamo noi
Le coordinate x, y e z sono semplicemente dei simboli. Di solito rappresentano coordinate spaziali, ma nulla impedisce di dargli un altro significato. Potrebbero, ad esempio, rappresentare le componenti R, G e B di un colore in un certo spazio colore RGB. Due diversi colori potrebbero quindi essere rappresentati simbolicamente come ![]() e
e ![]() . Nella rappresentazione più comune, i valori R, G e B sono interi positivi compresi tra 0 e 255, ma questo non cambia la sostanza delle cose. In armonia con quanto fatto per lo spazio tridimensionale euclideo, potremmo pensare di definire una distanza tra questi due colori come segue:
. Nella rappresentazione più comune, i valori R, G e B sono interi positivi compresi tra 0 e 255, ma questo non cambia la sostanza delle cose. In armonia con quanto fatto per lo spazio tridimensionale euclideo, potremmo pensare di definire una distanza tra questi due colori come segue:
(4) ![]()
Di nuovo varrebbe la regola che due colori (due punti) devono avere le stesse componenti per essere uguali. In quel caso, quella che potremmo chiamare la “distanza cromatica” tra loro sarebbe pari a 0. Abbiamo utilizzato un simbolo diverso da quello che si usa di solito, che è ![]() (o DeltaE). Questo perché la definizione data dalla (4) è formalmente corretta ma non si utilizza nella realtà, per un motivo sottile che vale la pena di esaminare.
(o DeltaE). Questo perché la definizione data dalla (4) è formalmente corretta ma non si utilizza nella realtà, per un motivo sottile che vale la pena di esaminare.
Il mondo è fatto a scale
Immaginiamo di dover salire una scala. Se gli scalini sono tutti uguali, avremo vita abbastanza facile; ma se gli scalini hanno altezze diverse le cose non sono così semplici.
Nella figura, la scala verde e la scala rossa partono dallo stesso livello e arrivano alla stessa quota, ma è molto più facile salire la prima che la seconda. Quando spostiamo il piede da uno scalino all’altro della scala verde, dobbiamo sempre alzarlo allo stesso modo; ciascuno scalino equivale, diciamo, a 10 unità. Nel caso della scala rossa, le unità a volte sono 13, a volte 15, a volte 8. Possiamo dire che sulla scala verde i passi sono uniformi, su quella rossa no.
Questo è un po’ come cercare di disegnare su un foglio suddiviso in rettangoli in cui ciascun rettangolo ha una dimensione diversa. Se affermassimo che ogni suddivisione corrisponde a 1 metro (ad esempio), avremmo segmenti le cui lunghezze appaiono diverse che però risultano uguali dal punto di vista dei numeri; oppure segmenti le cui lunghezze appaiono uguali che per risultano diversi dal punto di vista del valore numerico. In realtà talvolta questo è desiderabile: una scala logaritmica, ad esempio, viene usata per rappresentare grandezze la cui variabilità è così ampia da suggerire che una scala lineare non sia sufficiente. Su una scala logaritmica, tacche equidistanti possono assumere i valori 1, 10, 100, 1000… invece che 1, 2, 3, 4… (o qualsiasi sequenza lineare). Detto questo, salire una scala fisica i cui scalini abbiano la stessa altezza è semplice; in tutti gli altri casi è più difficile – o addirittura impossibile.
Cosa c’entra con il colore?
Questo problema riguarda anche il colore, perché il colore è qualcosa che percepiamo. Variazioni prevedibili e costanti quando ci spostiamo da un punto all’altro di uno spazio colore (in pratica, da un colore a un altro) sono assai desiderabili. Ciò che vogliamo è definire un DeltaE che abbia lo stesso significato in tutti i punti dello spazio, senza dare luogo a incoerenze percettive.
Partiamo da una semplice scala di grigi: in uno spazio colore RGB (ad esempio, sRGB) otteniamo un colore acromatico quando le tre coordinate sono uguali tra loro: R = G = B. Se vogliamo suddividere l’intervallo compreso tra 0 e 255 in dieci parti uguali, dobbiamo partire da 0 e aggiungere 25,5 ogni volta. Purtroppo non abbiamo a disposizione i numeri decimali, quindi ricorreremo a un’approssimazione: aggiungeremo alternativamente 25 e 26 per compensare, perdendo mezzo punto da una parte e riguadagnandolo dall’altra. In questo modo otteniamo la sequenza di valori 0, 25, 51, 76, 102, 127, 153, 178, 204, 229, 255. Questi undici valori definiscono dieci intervalli. Se creiamo una scala di grigi in cui le tre coordinate R, G e B siano uguali tra loro e assumano i valori riportati sopra, otteniamo quanto segue:
È ciò che ci aspettiamo: il nero corrisponde a (0, 0, 0), il bianco a (255, 255, 255), e in mezzo abbiamo dei toni di grigio più o meno chiari a seconda dei numeri che li caratterizzano. Osserviamo però la scala seguente:
A prima vista le due scale possono sembrare uguali, ma non è così. Proviamo ad affiancarle, creando una doppia scala in cui la parte superiore corrisponda a quella creata per prima e quella inferiore a quella creata per seconda:
Il nero e il bianco sono, naturalmente, identici. A ben guardare, si nota che il secondo riquadro è leggermente più chiaro nella scala inferiore. Nei rimanenti otto riquadri (dal terzo al penultimo), la scala superiore appare invece più chiara.
Quale delle due scale presenta una variazione più omogenea tra un riquadro e l’altro? La risposta è: la seconda. Dal punto di vista percettivo, le gradazioni di grigio appaiono spaziate più uniformemente. È come se la scala sottostante avesse tutti gli scalini della stessa altezza, e quella sopra avesse scalini di altezza variabile, come la scala rossa rappresentata nel grafico precedente.
L’idea è semplice: se partiamo da un quadrato interno qualsiasi e muoviamo un passo verso destra, ci ritroveremo in un quadrato più chiaro. Se ci spostiamo su un altro quadrato qualsiasi e muoviamo di nuovo un passo verso destra, vorremmo che la variazione di chiarezza fosse uguale alla precedente. Vorremo che gli scalini della scala avessero tutti la stessa altezza, in sostanza.
Alla ricerca dell’uniformità percettiva
Questa caratteristica prende il nome di uniformità percettiva. Proviamo a fare un esempio ulteriore:
In questo caso, la differenza è ancora più eclatante rispetto a prima. Il meccanismo è identico, ma stavolta abbiamo usato ProPhoto RGB invece di sRGB, e il risultato è diverso perché i due spazi hanno curve di contrasto diverse. La variazione tra i grigi appare certamente più omogenea nella scala in basso (identica alla precedente), e basta osservare i primi cinque quadrati della scala superiore per capire che la differenza di chiarezza tra un quadrato e il suo precedente non è la stessa per tutti i quadrati.
La scala inferiore deriva dallo spazio colore Lab. L rappresenta la grandezza fotometrica denominata chiarezza, e i quadrati della scala inferiore hanno valori compresi tra 0 e 100, intervallati di 10 in 10. L varia quindi secondo la sequenza 0, 10, 20, 30, …, 80, 90, 100. Tra un quadrato e il successivo, il DeltaE è costante e vale 10.
La scala superiore della figura precedente, derivante dalla suddivisione di ProPhoto RGB, ha i seguenti valori di chiarezza: 0, 13, 28, 40, 51, 60, 69, 77, 85, 93, 100. La sequenza dei DeltaE non è più costante: i valori sono rispettivamente 13, 15, 12, 11, 9, 9, 8, 8, 8, 7.
Le due scale viste nel grafico mostrato poco fa che riproponiamo qui sotto riportano semplicemente questi valori di chiarezza: la verde rappresenta Lab, la rossa rappresenta ProPhoto RGB. L’altezza dei singoli scalini è il valore del DeltaE nel passaggio da un campione di grigio al successivo.
In Lab, come già detto, la componente L rappresenta la chiarezza (in inglese: Lightness), le due componenti a e b sono invece puramente cromatiche: a ci dice quanto un colore tende al verde o al magenta, b ci dice quanto tende al blu o al giallo. Una delle caratteristiche di Lab, o meglio una sua aspirazione, è quella di essere percettivamente uniforme, ovvero – nel paragone della scala – di avere tutti gli scalini di altezza uguale. È un’aspirazione perché in realtà l’uniformità di Lab non è perfetta, ma di certo i suoi scalini sono più regolari di quelli di qualsiasi spazio RGB.
La formula del DeltaE 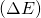
Dati due colori espressi in Lab dalle terne ![]() e
e ![]() , possiamo quindi definire la distanza tra essi per mezzo della seguente formula, in tutto e per tutto identica alla (3) se sostituiamo le variabili simboliche x, y e z con L, a e b:
, possiamo quindi definire la distanza tra essi per mezzo della seguente formula, in tutto e per tutto identica alla (3) se sostituiamo le variabili simboliche x, y e z con L, a e b:
(5) ![]()
Dal momento che Lab è abbastanza uniforme dal punto di vista percettivo, questa è una scelta migliore per definire la distanza tra due colori, che viene di norma indicata con il termine DeltaE. Bisogna però considerare una cosa, che è facile spiegare con un’immagine.
La figura è divisa in nove quadrati. Il quadrato centrale è quello di riferimento, che corrisponde al grigio 50% di Lab (50L 0a 0b). Gli otto quadrati che lo circondano hanno lo stesso valore di L e differiscono solo per le componenti cromatiche. I quattro quadrati posti nei punti cardinali (quelli immediatamente sopra, a destra, sotto e a sinistra del centro, in linea retta) hanno lo stesso DeltaE rispetto al quadrato centrale: il suo valore è 3. I quattro quadrati di angolo hanno invece un valore diverso, che è circa 4,24: ovvero, i quadrati di angolo sono cromaticamente “più distanti” da quello centrale rispetto agli altri quattro.
Consideriamo solo i quattro quadrati posti ai punti cardinali, ribadendo che la “distanza” del colore che rappresentano rispetto al quadrato centrale è identica per tutti. È facile comprendere che il DeltaE ci dice quanto siamo distanti, ma non dove siamo. È un po’ come se un amico ci chiamasse dicendo: “mi sono perso a 1 km da casa tua, da che parte devo andare per raggiungerti?” Non possiamo saperlo, a priori, perché non sappiamo in quale direzione si trovi rispetto a noi.
Tecnicamente, DeltaE è uno scalare: un numero, senza direzione. Di fatto, per sapere se stiamo errando verso il verde, il giallo, o un altro colore ci servirebbe un vettore: un numero, con una direzione e un verso (diciamo: un segno). Questo è uno dei limiti del parametro che viene spesso utilizzato per misurare lo scostamento cromatico di un campione rispetto a un campione dato – ma non è l’unico. Ne parleremo nella seconda parte di questo articolo.