Sono passati oltre due anni da quando ho scritto l’ultimo articolo su questo blog. Non intendevo abbandonarlo: semplicemente mi sono sentito poco stimolato a scrivere, per vari motivi. Uno di questi era la sensazione di avere in qualche modo esaurito gli argomenti principali. Riparto oggi, senza un piano preciso, dopo avere concluso un videocorso sul formato RAW per Teacher-In-A-Box, che uscirà presto. L’argomento di questo articolo fa parte di quel corso, e riguarda la differenza tra come un sensore digitale e il sistema visivo umano registrano la luce di una scena.
Nella giungla della fotometria
La fotometria è la branca della scienza che misura le caratteristiche della luce, in particolare la sua intensità e varie grandezze derivate. Non è materia semplice, soprattutto perché le grandezze utilizzate sono numerose e spesso vengono confusi: pochi hanno chiara la differenza tra energia luminosa, flusso luminoso, illuminamento, intensità luminosa, luminanza e altri termini complicati. Paradossalmente, l’unico termine di uso comune non è riconosciuto dalla fotometria: è il termine luminosità. Tutti istintivamente sappiamo interpretare una frase come “il tuo monitor appare più luminoso del mio”, oppure “quest’area della fotografia ha una luminosità superiore a quest’altra”, ma il concetto è mal definito.
Se vogliamo parlare di come un sensore digitale registra i dati di una scena, dobbiamo riferirci a una grandezza fisica detta luminanza. Formalmente, la luminanza è definita come l’intensità luminosa emessa da una superficie in una determinata direzione, divisa per l’area della superficie apparente. Già qui le cose si fanno complesse: si parla di “superficie apparente” perché non è detto che osserviamo la superficie emittente frontalmente, e la sua area sembra variare (anche se geometricamente rimane costante) a seconda dell’angolo di osservazione.
Il fattore di luminanza
In generale, una superficie riflette parte della luce che incide su di essa. La luminanza si misura in candele su metro quadrato (cd/m2), ma a prescindere da questo possiamo calcolare il rapporto tra luminanza riflessa e luminanza incidente. Il rapporto tra le due quantità (luminanza riflessa) / (luminanza incidente) è detto fattore di luminanza, ed è una grandezza fisica adimensionale, priva di unità di misura. La figura mostra il fenomeno della riflessione.
Immaginiamo ora che una luce di determinata intensità, emessa da una sorgente, incida su una superficie e venga totalmente riflessa. Immaginiamo anche di osservare il fenomeno frontalmente, in maniera da non doverci preoccupare dell’area apparente della superficie. “Totalmente riflessa” implica che la superficie non assorba alcuna energia dalla luce che la colpisce: in pratica, dev’essere perfettamente bianca. In questo caso, la luminanza emessa dalla superficie (che noi vediamo come emettitore, anche se in realtà l’emissione avviene altrove) è identica alla luminanza incidente su di essa. È un modo complicato di affermare che la superficie che stiamo esaminando riflette il 100% della luce che riceve, ed è probabilmente più semplice ragionare in termini di percentuale. Una superficie simile apparirebbe perfettamente bianca. Il rapporto a cui abbiamo accennato, (luminanza riflessa) / (luminanza incidente), è uguale a 1, ovvero 100%. La figura illustra questo specifico caso.

All’estremo opposto, potremmo avere una superficie che assorbe tutta la luce che la colpisce. In questo caso, il fattore di luminanza vale 0, ovvero 0%. La superficie appare perfettamente nera. Anche qui, la figura funge da esempio.

L’occhio e il sensore digitale
Immaginiamo di avere una serie di coloranti grigi di tono diverso, dal più scuro al più chiaro. Ci proponiamo di creare una scala con undici gradini in cui il primo sia completamente nero e l’ultimo perfettamente bianco: fattore di luminanza, rispettivamente, 0% e 100%. I nove gradini intermedi verranno colorati in modo che, strumentalmente, misuriamo nel secondo un fattore di luminanza del 10%, nel terzo del 20% e così via, fino al penultimo che dovrà avere un fattore di luminanza del 90%.
Ci immaginiamo che la scala dovrebbe avere più o meno questo aspetto:

In effetti, questo è ciò che vedrebbe un sensore. In un sensore digitale, ciascun fotosito è un contatore di fotoni, ovvero delle particelle elementari che costituiscono il campo elettromagnetico che noi chiamiamo “luce”. Il numero di fotoni è proporzionale alla luminanza, e quindi al fattore di luminanza (se la luce incidente rimane costante, naturalmente). Per fare un esempio, un fotosito ideale in grado di contare al massimo 1.000 fotoni ne conterebbe 500 in corrispondenza di un fattore di luminanza del 50%, e 730 se il fattore di luminanza fosse invece del 73%. Esiste quindi una proporzionalità diretta tra il fattore di luminanza che colpisce il fotosito di un sensore digitale e il numero che quel fotosito genera.
Il problema è che purtroppo il nostro sistema visivo la pensa diversamente. Se noi osservassimo la scala di grigi costruita come descritto poco fa, vedremmo una cosa ben diversa:

La differenza dalla scala precedente è eclatante. Per semplicità, affianchiamo le due scale:

Fotometria o percezione?
La scala superiore è quella che rappresenta il fattore di luminanza misurato dal sensore, la seconda è ciò che il nostro sistema visivo vedrebbe guardando quella scala. Si nota subito come, nel caso della visione umana, le parti scure tendano a differenziarsi moltissimo, mentre la transizione tra le parti più chiare sia molto morbida. Si noti che la scala superiore è espressa in percentuale, mentre quella inferiore in numeri che vanno da 1 a 100.
La seconda scala, infatti, si riferisce alla chiarezza, una grandezza percettiva legata al fattore di luminanza ma dal comportamento ben diverso. Il nome per esteso della chiarezza è “chiarezza CIE 1976 (L*)” e il suo rapporto con il fattore di luminanza è definito nel documento CIE 15:2004 Colorimetry. Come spesso accade in fotometria, la formula è abbastanza complessa, ma in maniera molto approssimata possiamo dire che la chiarezza è proporzionale alla radice cubica del fattore di luminanza, tranne che nelle aree più scure in cui la relazione è diversa. Il fattore di proporzionalità è 100 (NB: in realtà è 116, ma viene manipolato in modo che la chiarezza massima, il “bianco”, corrisponda a L* = 100). Un grafico aiuta a comprendere come stanno effettivamente le cose.
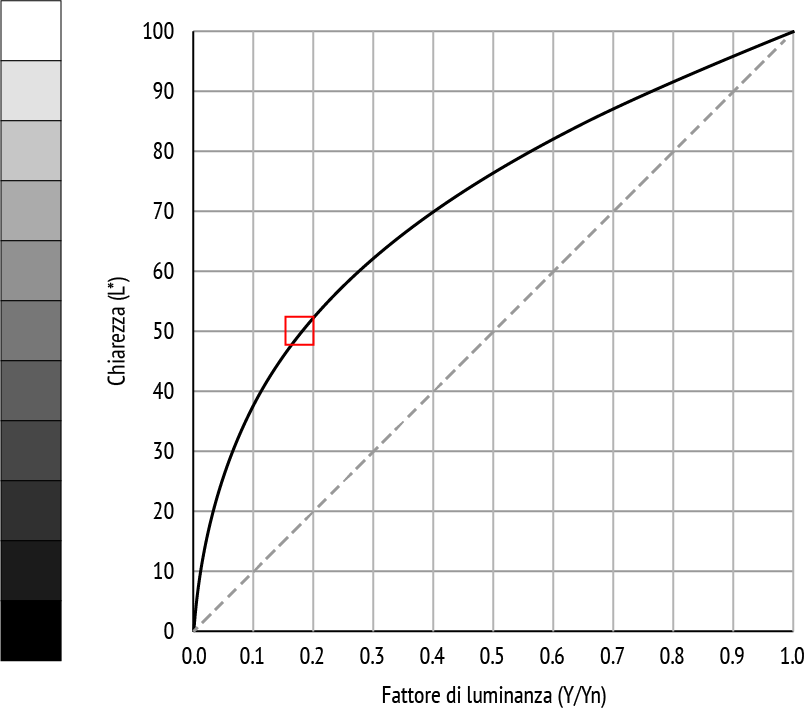
Se chiarezza (ciò che percepiamo) e fattore di luminanza (ciò che misuriamo) fossero uguali, la curva di risposta del nostro occhio sarebbe la linea tratteggiata che attraversa il grafico. Ovvero, vedremmo esattamente ciò che “vede” un sensore digitale. Dal momento che non sono uguali, dobbiamo affidarci alla curva rappresentata con linea continua. La scala sulla sinistra mostra l’aspetto (all’occhio umano) dei grigi legati a valori di chiarezza pari a 0, 10, 20… fino a 100. Il grigio corrispondente a L* = 50 è quello che il nostro sistema visivo percepisce come equidistante, ovvero “a metà strada”, tra il nero (L* = 0) e il bianco (L* = 100). È quello che i fotografi chiamano grigio medio.
Grigio al 18%?
Sorprendentemente, il fattore di luminanza che genera la sensazione di un grigio con L* = 50 in noi è bassissimo: se scendiamo dal quadratino rosso sull’asse orizzontale, scopriamo che è sufficiente un fattore di luminanza pari a 0,18. Ecco quindi svelato il perché la famosa “gray card” della Kodak viene definita anche “cartoncino grigio 18%”: riflette pochissima luce rispetto a quella che incide su di esso, ma il nostro sistema visivo percepisce una chiarezza di gran lunga superiore a L* = 18.
Questo fatto ha una ricaduta: se potessimo osservare la mappa dei fattori di luminanza prodotta da un sensore digitale vedremmo dei rapporti tonali completamente sbagliati. Per questo, a prescindere dall’esistenza del colore, i dati RAW registrati dal sensore vanno processati per mezzo di una curva che li trasformi in dati che offrano una coerenza tra la chiarezza percepita della scena e quella che invece percepiamo nella fotografia. Questa è una delle operazioni che avvengono quando sviluppiamo un’immagine RAW.
L* è la stessa L di Lab
Per chi avesse dei dubbi, la L* che indica la chiarezza è la stessa che compare quando si lavora nel metodo colore Lab. Quando affermiamo che in Lab il grigio medio è definito dalla terna (50, 0, 0) dove i numeri rappresentano i valori, in ordine, di L, a e b, stiamo facendo un’affermazione corretta.
Purtroppo RGB, un metodo colore a cui siamo più abituati, complica le cose. La terna (128, 128, 128) che si utilizza di norma per definire il grigio medio, in generale non ha lo stesso aspetto di L* = 50. Quel che è peggio, l’aspetto dipende dallo spazio colore. In sRGB, il “grigio medio” proposto da Photoshop ha un aspetto più chiaro (L* = 54). In ProPhoto RGB, ancora più chiaro (L* = 61). Questo dipende da un piccolo e confusionario parametro presente all’interno del profilo ICC che definisce questi spazi colore: il famigerato gamma. Magari ne parleremo un’altra volta…


Ciao Marco, articolo come sempre illuminante, in tutti i sensi.
Quando scriverai un articolo sul Gamma, come accennato a fine post, sarò il primo in assoluto a leggerlo perché ho il sospetto che con te finalmente mi sarà chiaro.
Intanto se mi risolvi questo mistero epocale te ne sarei grato: è giusto affermare che, in RGB, i dati dell’asse x esprimono la luminanza per ogni singolo canale R, G e B?
Grazie e buon lavoro
Andrea, scusa innanzitutto l’immenso ritardo della mia risposta: il commento mi era completamente sfuggito – sorry!
Per quanto riguarda la tua domanda, se pensi a un sistema di assi cartesiani (xyz) in cui facciamo coincidere i singoli assi con le coordinate RGB, la tua affermazione è corretta. Lo spazio colore RGB diventa un cubo, con il nero nell’origine (0, 0, 0) e il bianco nel vertice più distante da essa (255, 255, 255) – naturalmente se pensiamo in 8 bit. Questo è un sistema discreto, perchè gli stimoli di colore possono avere solo coordinate intere: non esiste in esso un valore come (127.5, 127.5, 127.5), per capirci. In alternativa, possiamo pensare di normalizzare i valori massimi a 1 e usare numeri reali, ovvero “con la virgola”, ma il concetto non cambia. Questo diventa un sistema continuo, naturalmente: ogni valore compreso tra 0 e 1 è lecito.
Un caro saluto!
MO