Uno spazio aperto
Quando ho iniziato a scrivere in questo blog, qualche mese fa, speravo che avrebbe potuto nascerne una specie di spazio aperto per discussioni sul colore: spazio unilateralmente moderato, lo ammetto, ma gli oltre trecento commenti comparsi a seguito dei miei post negli ultimi mesi mi lasciano ben sperare per il futuro. Alcuni di questi commenti sono per me particolarmente interessanti, perché impattano casualmente (o forse no) su argomenti sui quali sto meditando da un po’ di tempo. Il mio ultimo articolo, ad esempio, ha suscitato un commento da parte di Luca Negri che riporto qui sotto:
I canali a e b mi appaiono allora non come dei primari ma come il risultato di una elaborazione che mi sta ad indicare le rispettive quantità di R di G e di B.
Luca si riferisce naturalmente ai canali a e b di Lab. Quello che Luca si chiede, in sostanza, è se sia possibile e sensato codificare questi canali in funzione di R, G e B. La risposta più corretta è no, perlomeno non direttamente. Il sito di Bruce Lindbloom, nella sezione Math, riporta le formule per la conversione standard da RGB a XYZ, e poi da XYZ a Lab. XYZ, il cui nome completo è CIE 1931 XYZ, è uno spazio colore intermedio che non discuteremo in questa sede; se siete interessati a capire come funziona potete trovare delle informazioni qui.
Quello che a me interessa, però, è la possibilità di creare dei canali che abbiano proprietà simili a quelle dei canali Lab, in particolare di a e b, all’interno di RGB. A cosa possono servire? A molte cose, certamente, in primis la realizzazione di alcune maschere migliori di quelle ottenibili con gli strumenti nativi a disposizione in RGB e senza passare per un duplicato del documento convertito in Lab; ma non solo. In generale, però, è un esercizio interessante dal punto di vista concettuale perché richiede di immaginare come possano essere realizzati i canali a e b e poi richiede di costruirli direttamente in Photoshop con gli strumenti a disposizione. Se l’esercizio è svolto bene, e ci sono diversi modi per farlo, è anche un’elegante applicazione di tecnica perché sfrutta a fondo alcune caratteristiche di solito poco usate di certi strumenti disponibili in Photoshop.
Cosa sono i canali Bogus?
L’idea di creare dei canali fasulli che imitino quelli di altri metodi colore non è nuova. Da anni Dan Margulis ha introdotto l’idea del Bogus black, ovvero il falso nero, che è una manipolazione del canale K di CMYK ottenuta convertendo un documento in tale spazio colore e imponendo alla conversione parametri che sarebbero piuttosto improbabili nel mondo reale. In senso stretto, non si tratta esattamente di un canale fasullo: il Bogus black è a tutti gli effetti un canale CMYK, solo che appartiene a una variante di CMYK che di fatto non avrebbe senso utilizzare nella pratica quotidiana. Si avvicina di più a questo concetto il canale Ersatz black introdotto sempre da Margulis in una delle azioni del flusso di lavoro PPW (in particolare, in H-K): è un canale del nero fittizio creato esclusivamente a partire da R, G e B con operazioni successive di applicazione di un canale sull’altro in metodo di fusione Scolora. Quello che mi interessa oggi è questo: creare in RGB due canali alfa che, senza essere i veri a e b di Lab, siano in qualche modo assimilabili a essi. E tutto questo, naturalmente, senza mai uscire dallo spazio colore in cui sto lavorando. Li chiamerò Bogus a e Bogus b, in onore alla terminologia di Dan Margulis.
Ci serve anche un Bogus L?
Iniziamo togliendoci un incomodo dal tavolo: perché solo a e b e non L? La risposta è che la vera peculiarità di Lab, rispetto a RGB, è quella di separare il colore dalla luminosità. In RGB abbiamo quasi infinite combinazioni per creare luminosità alternative a quella standard proposta da Photoshop: possiamo utilizzare la regolazione Miscelatore canale, o applicare un canale sull’altro in maniera creativa e selettiva con metodi di fusione come Scurisci e Schiarisci, o utilizzare la regolazione Bianco e nero, o ancora Mappa sfumatura. C’è solo l’imbarazzo della scelta. Quello che invece manca in RGB è un’informazione sul colore separata dal resto: è possibile ottenerla, in parte, per mezzo del metodo di fusione Colore fondendo un’immagine con un livello a luminosità costante, ma non è quello che ho in mente. In ogni caso, non credo che costruire un canale L fittizio in RGB sarebbe particolarmente utile, vista la pletora di possibilità che già abbiamo; perlomeno non utile come costruire due pseudo-canali a e b.
Un modello semplice di Lab
Prima di partire, un’avvertenza. Nel seguito ho riportato tutti i passaggi, a volte in maniera un po’ pedante, per permettere a tutti di seguire bene il ragionamento. In realtà alcune parti non sono essenziali, specialmente quelle in cui riformulo le equazioni che definiscono i canali Bogus. Se trovate noiosi certi passaggi è semplicemente perché lo sono, e potete tranquillamente saltarli, perché sono elementari e sono stati inseriti per completezza. Attenzione, però: nel corso dell’esposizione ci sono alcune discussioni abbastanza sottili sul perché certe operazioni funzionino solo se svolte in una certa sequenza, e a mio parere quelle sono interessanti perché svelano alcune caratteristiche nascoste di certi metodi di fusioni.
Il modello che ho in mente è molto semplice, al punto di essere rozzo. Nel tentativo di imitare il modello a colori opponenti di Hering, il mio canale Bogus a dovrà contenere le informazioni dell’asse verde-magenta, con i valori negativi a indicare la tendenza al verde e quelli positivi la tendenza al magenta. Inoltre dovrà essere neutro per a = 0. Il canale b si comporta allo stesso modo, lungo l’asse blu-giallo. In RGB abbiamo già un primario verde e uno blu, anche se la loro cromaticità è diversa rispetto al verde e al blu di Lab, e si tratta di sintetizzare gli altri due colori che ci servono. La cosa più ovvia è provare a definire (simbolicamente) M = R + B e Y = R + G. La mia idea è quella di provare a costruire i canali Bogus a e Bogus b come segue (li abbrevio con le sigle a e b, per brevità):
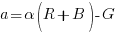
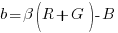
I coefficienti 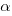 e
e 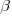 sono necessari per la condizione di neutralità, come vedremo tra poco. Scopriremo anche che sono uguali; li possiamo calcolare semplicemente imponendo quanto segue: per R = G = B vogliamo avere a = 0 e b = 0. Per fare questo, basta ipotizzare che il valore comune ai canali R, G e B sia X, con X un numero qualsiasi compreso tra 1 e 255. Escludo la possibilità che X sia uguale a 0, perché in quel caso tutti e tre i canali sarebbero uguali a 0 e i coefficienti
sono necessari per la condizione di neutralità, come vedremo tra poco. Scopriremo anche che sono uguali; li possiamo calcolare semplicemente imponendo quanto segue: per R = G = B vogliamo avere a = 0 e b = 0. Per fare questo, basta ipotizzare che il valore comune ai canali R, G e B sia X, con X un numero qualsiasi compreso tra 1 e 255. Escludo la possibilità che X sia uguale a 0, perché in quel caso tutti e tre i canali sarebbero uguali a 0 e i coefficienti 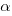 e
e 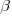 che cerchiamo sparirebbero dall’equazione; questo però non influenza il risultato finale. Sostituendo X a R, G e B, la prima equazione riportata sopra diventa:
che cerchiamo sparirebbero dall’equazione; questo però non influenza il risultato finale. Sostituendo X a R, G e B, la prima equazione riportata sopra diventa:
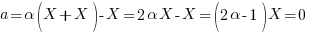
Dal momento che X può assumere qualsiasi valore tra 1 e 255, questo implica che sia:
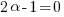
ovvero, 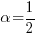 . Un calcolo identico ci porta a concludere che deve valere anche la condizione
. Un calcolo identico ci porta a concludere che deve valere anche la condizione 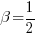 . Le nostre equazioni diventano quindi:
. Le nostre equazioni diventano quindi:
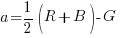
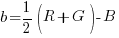
Vogliamo ora capire che valori assumono a e b in corrispondenza dei colori primari e secondari di RGB. In altri termini, vogliamo sapere come vengono tradotti in questo spazio pseudo-Lab i colori rosso, verde, blu, ciano, magenta e giallo. La prima cosa che dobbiamo tenere presente è che, negli spazi reali, le cromaticità dei primari di RGB e dei colori che hanno lo stesso nome in Lab sono diverse. Ricordando che in Lab un valore racchiuso tra parentesi corrisponde a un numero negativo, possiamo dire che in Adobe RGB, ad esempio, 255R0G0B si traduce in 54L81a70b: a e b non sono uguali, eppure noi definiamo “rosso” un colore che abbia a = b. Il problema sta nella limitatezza del linguaggio per cui “rosso” non è di per sé un colore ben definito quanto una categoria molto ampia di colori diversi. Per il verde la differenza è ancora più clamorosa: 0R255G0B si traduce in 88L(79)a81b, e la componente gialla in b è addirittura maggiore di quella verde in a. Stesso discorso vale per il blu: 0R0G255B si traduce in 30L68a(112)b, certamente non un colore puro nel canale b. Tutto questo per dire che dal momento che il nostro pseudo-Lab è costruito a partire dai primari di RGB, sarà impossibile che l’aspetto dei canali Bogus sia identico a quello dei canali dello spazio Lab “vero”.
Applicando le formule viste sopra, le corrispondenze dei primari di RGB e dei secondari sono le seguenti (NB: alcuni risultati formalmente avrebbero la virgola; vengono applicate le approssimazioni opportune e non viene indicata la componente L, che stiamo ignorando):
- Rosso: 255R0G0B si traduce in 128a128b
- Verde: 0R255G0B si traduce in (255)a128b
- Blu: 0R0G255B si traduce in 128a(255)b
- Ciano: 0R255G255B si traduce in (128)a(128)b
- Magenta: 255R0G255B si traduce in 255a(128)b
- Giallo: 255R255G0B si traduce in (128)a255b
Sono numeri un po’ strani se li confrontiamo con quelli che siamo abituati a leggere in Lab, e infatti manca una normalizzazione (ovvero un fattore di scala) perché alcuni valori arrivano a 255, mentre noi siamo abituati a lavorare con numeri Lab che non escono dall’intervallo compreso tra -128 e 127. Questo accade perché abbiamo solo imposto una condizione di neutralità senza vincolare in alcun modo l’intervallo. La mia impressione è che se riscriviamo le equazioni come segue, allo scopo di contenere i valori più elevati (in valore assoluto) all’interno di un range più familiare, tutto andrà a posto:
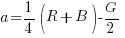
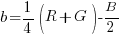
La tabella sopra riportata diventa infatti:
- Rosso: 255R0G0B si traduce in 64a64b
- Verde: 0R255G0B si traduce in (128)a64b
- Blu: 0R0G255B si traduce in 64a(128)b
- Ciano: 0R255G255B si traduce in (64)a(64)b
- Magenta: 255R0G255B si traduce in 128a(64)b
- Giallo: 255R255G0B si traduce in (64)a128b
Tutto molto più sensato, se escludiamo il fatto che il numero 128 non è compreso nell’intervallo – ma è un problema minore perché in via eccezionale possiamo benissimo arrotondare per troncamento, e non per approssimazione, il risultato originale: 127,5 diventerà 127. Possiamo certamente convivere con una differenza di un punto all’estremo del range.
Questo può andare bene dal punto di vista teorico, ma non da quello pratico: quello che noi vogliamo fare è costruire dei canali. I canali sono immagini con 256 livelli di grigio identificati dai numeri compresi tra 0 e 255, e i numeri negativi non sono contemplati. Dobbiamo quindi applicare un cosiddetto offset alle formule, ovvero uno spostamento che muova tutti i valori ottenuti nell’ultima tabella all’interno di un intervallo plausibile per un’immagine in scala di grigio. La cosa più ovvia da fare è riscrivere ancora una volta le formule in questo modo:
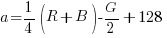
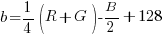
Ed ecco come questo ridefinisce i valori:
- Rosso: 255R0G0B si traduce in 192a192b
- Verde: 0R255G0B si traduce in 0a192b
- Blu: 0R0G255B si traduce in 192a0b
- Ciano: 0R255G255B si traduce in 64a64b
- Magenta: 255R0G255B si traduce in 255a64b
- Giallo: 255R255G0B si traduce in 64a255b
Qualsiasi valore neutro, caratterizzato da R = G = B, si traduce semplicemente in 128a128b. Tutto questo può sembrare molto strano, ma è corretto: se invece che pensare ai numeri Lab come li conosciamo li interpretiamo come valori RGB in un’immagine in scala di grigio, tutto torna. a < 0, ad esempio, diventa a < 128, così come b > 0 diventa b > 128. Se vi riferite al discorso che ho fatto sui sistemi di riferimento nel mio precedente articolo, tutto ciò che abbiamo fatto è spostare l’origine del sistema di riferimento in un punto che ci fa comodo.
Armiamoci e partite: costruire i canali Bogus
Il problema adesso è realizzare materialmente i canali. Potete evitare il lungo lavoro necessario a scrivere un’azione opportuna, scaricando da qui quella che io ho scritto e predisposto, ma vale forse la pena di delineare come sia possibile raggiungere il risultato. [NB: dovete scaricare il documento collegato al link qui sopra, non limitarvi ad aprirlo; nel secondo caso vedrete il contenuto dell’azione nel browser, ma non avrete il file che vi serve.] Se prendiamo la formula definitiva di a, il suo significato è questo:
Parti con un canale vuoto (ovvero, nero), aggiungi i valori del canale R divisi per 4, aggiungi quelli del canale B divisi per 4, sottrai quelli del canale G divisi per 2 e aggiungi 128.
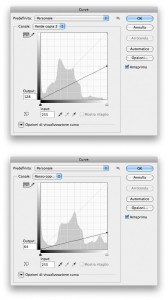
Già: ma come si fa a dividere un canale per un numero fisso? Se guardiamo alle formule scritte sopra sembra che ci servano cinque canali temporanei per costruire i nostri (falsi) a e b: tre canali che contengano i valori di R, G e B divisi per quattro, più due canali che contengano i valori di G e B divisi per due. Questa è senza dubbio una strada possibile, e uno dei modi per ottenere questo risultato è utilizzare delle curve che probabilmente non utilizzeremmo mai nella vita reale. Per dividere un canale per due, si può procedere come segue: duplichiamo il canale e utilizziamo la prima delle due curve che vedete qui a fianco. Questa curva è definita da due soli punti, che sono i suoi punti estremi. Il primo (a sinistra) non ha alcun effetto, in quanto impone che il valore di input 0 rimanga tale; il secondo (a destra) porta invece il valore di input 255 a un output 128, ovvero lo divide per due salvo la solita approssimazione (127,5 non esiste, in RGB, e si approssima a 128). È facile rendersi conto che tutti i valori intermedi vengono trattati allo stesso modo grazie al fatto che la curva è lineare. Questo causerà naturalmente una posterizzazione, anche se praticamente invisibile, dovuta al fatto che alcuni pixel originariamente diversi diventeranno uguali dopo l’applicazione della curva: ad esempio, una luminosità pari a 49 (sto pensando in RGB) e una luminosità pari a 50 verranno entrambe tradotte in una luminosità pari a 25. Di fatto, l’immagine che otteniamo è codificata con 7 bit al massimo, non 8. La curva in basso nella figura fa esattamente la stessa cosa: il punto di sinistra rimane intatto, il punto di destra porta il valore di input 255 a un output 64: è una divisione per quattro. Anche qui, posterizzazione (più grave) per gli stessi motivi – l’immagine risultante è codificata con 6 bit al massimo. La posterizzazione non dipende di per sé dalle curve: qualsiasi altra tecnica che utilizziamo per schiacciare 256 livelli di grigio in uno spazio che può contenerne metà, o metà della metà, causerà questo effetto.
Ordine, disciplina!
A mio modo di vedere il metodo delle curve è poco elegante e non molto efficace. Tutto si può fare molto più rapidamente in un altro modo, che per manifestarsi in maniera chiara richiede una semplice riscrittura delle equazioni riportate sopra. Prima di discuterlo, però, devo segnalarvi un problema nascosto che non è affatto evidente a prima vista. Se noi interpretiamo simbolicamente le equazioni che abbiamo scritto, l’ordine in cui svolgiamo le operazioni non è importante perché somma e sottrazione sono commutative: in algebra, scrivere (x + y – z) o (y – z + x) è irrilevante. Non in Photoshop, però: bisogna stare molto attenti perché c’è un’insidia che ci attende. Ve la mostro con un esempio. Supponiamo di voler calcolare a mano il valore assunto da a, secondo l’ultima formula riportata, in corrispondenza della terna RGB definita da 60R140G200B. Se sostituiamo i valori nell’equazione otteniamo:
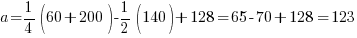
In Photoshop siamo in qualche modo costretti a fare le operazioni una alla volta, e la sequenza è questa:
- Dividiamo i canali (con una qualche tecnica) per i fattori che ci servono. I numeri riportati sopra diventano, nell’ordine, 60/4 = 15 (R/4), 140/2 = 70 (G/2), 200/4 = 50 (B/4).
- Sommiamo i contributi del rosso e del blu: 15+50 = 65.
- Sottraiamo il verde: 65-70 = -5.
- Aggiungiamo l’offset: -5+128=123.
Corretto? No, purtroppo: dal momento che viviamo in un intervallo che va da 0 a 255, il risultato della terza operazione è incomprensibile per Photoshop. Non esiste una luminosità negativa, in RGB. Quando chiediamo al programma di effettuare quell’operazione, la sua reazione davanti a qualcosa che non può ottenere è quella di sostituire il valore con la cosa più sensata che riesce a pensare: “ho 65 punti di luminosità, ne devo togliere 70… assurdo: tolgo tutto il possibile, ovvero 65, e non ci penso più”. Il risultato che Photoshop fornisce, quindi, è 0, e naturalmente non si sogna di segnalarci che ha compiuto un’approssimazione brutale. Quindi il risultato dopo l’applicazione dell’offset è 128, non 123. Questo perché l’operazione di somma, in Photoshop, è definita in maniera diversa rispetto a quello che intuitivamente penseremmo. Una definizione colloquiale è la seguente:
Se il risultato della somma è compreso tra 0 e 255, tienilo. Se è inferiore a 0, impostalo a 0. Se è superiore a 255, impostalo a 255.
Ovvero, con meno gentilezza e formalismo: “se è il caso, clippa pure senza pietà il risultato”. Questo è potenzialmente catastrofico nel momento in cui stiamo cercando di costruire un canale, perché alcune parti potrebbero avere dei valori falsati in maniera anche molto pesante. Si richiede quindi un intervento intelligente, che in realtà è facile da attuare. Se consideriamo che un canale può contenere soltanto valori tra 0 e 255, quel canale con i valori divisi per 4 conterrà al massimo valori compresi tra 0 e 64. Nel caso peggiore, la somma dei due contributi di R e B nella formula vista poco fa potrà valere 0. Se aggiungiamo ora l’offset, prima di sottrarre il contributo di G (che sarà compreso tra 0 e 128, perché G è diviso per 2), otteniamo come minimo 128. Qualsiasi cosa sottraiamo a questo punto sarà all’interno del range che ci serve, in quanto il risultato più piccolo possibile è 0: niente numeri negativi. Nel caso opposto, se R e B fossero al massimo, il loro contributo sommato sarebbe pari a 128. Aggiungiamo l’offset: otteniamo 256 – che corrisponde a un clipping di un solo valore all’estremo superiore della luminosità: credo che possiamo sopportarlo. Sottraiamo il caso peggiore di G/2 (ovvero, 128) e siamo a 128 di nuovo: quindi tutto ricade comunque nel range che ci serve. In buona sostanza, l’equazione va riscritta in questo modo: prima si sommano i contributi di R e B, poi si aggiunge l’offset, e infine si sottrae il contributo di G. In questo modo, tutto funziona. Proviamo a rifare l’esempio che ho portato poco fa:
- Sommiamo i contributi del rosso e del blu: 15+50 = 65.
- Aggiungiamo l’offset: 65+128 = 193
- Sottraiamo il verde: 193-70 = 123.
Questa volta non ci sono problemi, e naturalmente questo discorso vale in maniera assolutamente identica per la formula che definisce b. Vado dunque a riscrivere le equazioni con i termini nell’ordine giusto. In aggiunta, cambio la forma del primo termine in maniera da poter implementare poi la tecnica che ho in mente. Le formule diventano:
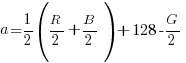
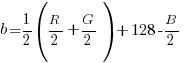
Istintivamente questa formula mi piace assai, perché se guardo solo ai contributi non mi servono più cinque canali temporanei, ma soltanto tre: ovvero, tre canali alfa che contengano i valori originali di R, G e B divisi per due. Come posso costruirli?
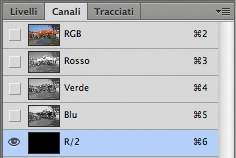
È più semplice di quanto sembri, e se volete provare vi servono soltanto due manovre. La prima: dopo avere aperto il Pannello Canali, cliccate sull’icona in basso a destra che vi consente di creare un nuovo canale alfa. Tenete premuto il tasto Alt, mentre cliccate: questo vi permetterà di dare un nome al canale, che chiamerete R/2. Notate che il canale viene creato completamente nero per default, il che significa che il suo valore di luminosità è ovunque pari a 0, se lo pensiamo in RGB. Questo ci suggerisce la seconda manovra, che serve per inserire nel canale ciò che vogliamo ottenere.
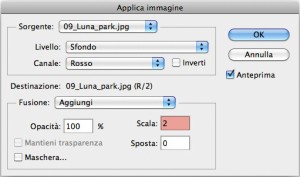
Il canale R/2 è già selezionato. Menu Immagine -> Applica immagine. Quello che ci serve è il canale R con i valori divisi per due. Il metodo di fusione Aggiungi, che è a tutti gli effetti una somma (anche se viziata dal potenziale clipping che ho analizzato poco fa – ma sappiamo di essere immuni al problema), ha due parametri in comune con il metodo di fusione Sottrai: Scala e Sposta. Aggiungi e Sottrai sono gli unici due metodi di fusione ad avere questi parametri, in Applica immagine. Il fattore Scala può essere compreso tra 1,000 e 2,000, può avere al massimo tre decimali e fa quanto segue: i valori del canale selezionato come sorgente, in questo caso R, vengono aggiunti ai valori del canale destinazione, che per noi è R/2, e la somma viene divisa per il fattore di scala. Se il fattore, come in figura, è 2, la somma viene divisa per due. A costo di essere noioso, riscrivo: la somma viene divisa per 2, e ribadisco questo perché ci sono cascato in pieno anch’io qualche anno fa – e non me ne sono dimenticato. Istintivamente si potrebbe pensare che i valori della sorgente vengano divisi per 2 e poi aggiunti al canale destinazione, ma non è così: la divisione avviene dopo che è stata fatta la somma. In realtà nel nostro caso tutto funziona, perché il canale destinazione è uniformemente popolato da pixel che hanno valore 0. Quindi, la somma di 0 con R genera semplicemente R, e la divisione di questo risultato per due genera R/2. Replichiamo la stessa identica procedura creando un canale G/2 e un canale B/2, e applicando G e B allo stesso modo, e avremo i tre canali temporanei che ci servono. Aggiungo che esiste anche un altro modo per dividere per due i valori di un canale: applicare il canale da dividere a un canale riempito di nero, in metodo di fusione Normale, al 50%. Come spesso accade Photoshop offre diverse strade per giungere allo stesso risultato, e ognuno può scegliere quella che preferisce.
Chiunque abbia un minimo trascroso nell’informatica soffre di un’attrazione fatale per l’eleganza e la compattezza. Se esiste un codice in grado di compiere un’operazione in maniera più semplice di un altro, quel codice è istintivamente percepito come migliore. Quello che voglio fare ora è creare in un solo passaggio un canale che contenga i primi tre termini dell’espressione che definisce il nostro canale Bogus a: in pratica, 1/2(R/2+B/2)+128.
Calcoli: prendi tre, paghi due
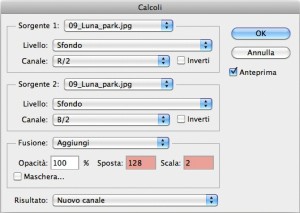
Questa operazione la affido al vecchio comando Calcoli. Abbiamo già creato i canali R/2, G/2 e B/2. Menu Immagine -> Calcoli e selezioniamo i due canali sorgente: R/2 e B/2. L’ordine è irrilevante, perché la somma è commutativa. Metodo di fusione: Aggiungi. Il fattore di scala, pari a 2, funziona esattamente come in Applica immagine: le due sorgenti vengono sommate e la somma viene divisa per due. Il parametro Sposta è l’offset che ci serve, e vale 128. Per completezza, i valori ammessi per il parametro Sposta sono interi compresi tra -255 e 255. Lo spostamento viene applicato dopo la somma e la divisione (notate come questo sia anti-intuitivo guardando l’interfaccia: le caselle Scala e Sposta andrebbero scambiate di posto). Il risultato viene inserito in un nuovo canale, che per default si chiamerà Alfa 1. Diamo OK e rinominiamo il canale appena creato come Bogus a. Ci resta una sola operazione da fare: sottrarre G/2. Possiamo farlo di nuovo con Applica immagine: non mostro la finestra di dialogo perché la logica dell’operazione dovrebbe essere già chiara: Bogus a è già selezionato, e applichiamo G/2 con metodo di fusione Sottrai, fattore di scala 1 e naturalmente nessun offset (Sposta = 0). Abbiamo finito: Bogus a contiene a questo punto il nostro primo finto canale Lab. Ripetendo la procedura selezionando i canali sorgente opportuni possiamo creare Bogus b. I tre canali temporanei non ci servono più, a questo punto, e li possiamo eliminare.
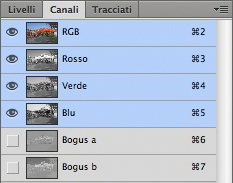
Alla fine dell’operazione, il pannello canali si presenta come nella figura a fianco. I tre canali originali sono intatti, e questo è necessario per evitare qualsiasi alterazione dell’immagine; in più abbiamo due canali che rappresentano il falso a e il falso b che abbiamo creato. Ribadisco: non sono i canali a e b, naturalmente, ma hanno delle caratteristiche in comune con essi che li rendono molto simili e che possono risultare utili nel momento in cui non vogliamo tanto codificare il colore in Lab quanto utilizzare i canali come sorgenti per maschere o per fusioni esoteriche con i canali RGB o addirittura con il composito RGB.
Cosa abbiamo comprato
A questo punto è ora di vedere i risultati di tutto questo lavoro. L’immagine originale che voglio esaminare è la seguente:

Qui di seguito, la comparazione tra i canali a e b di Lab ottenuti tramite una conversione diretta dell’originale, e i canali Bogus a e Bogus b generati dalla nostra azione:

Alcune parti dei canali sono palesemente diverse, ma la parentela è evidente: i gemelli cattivi che abbiamo creato potrebbero benissimo essere scambiati a prima vista per gli originali. Ci sono alcune differenze importanti: una è riscontrabile, ad esempio, nella scritta “Circus”, che nell’originale è gialla e tendente all’arancione. Questo implica che il canale a debba essere più chiaro del grigio al 50% in quell’area, perché dev’esserci una componente magenta: infatti, così è. Il canale Bogus a invece è più scuro. Questo dipende dal fatto che i primari che utilizziamo sono diversi: come il verde di RGB è diverso da quello di Lab, lo stesso accade per il magenta. Quello che chiamiamo magenta puro in RGB contiene una componente blu che lo rende più simile al viola: la tinta del magenta puro in Lab è più calda. Un’altra differenza è che il canale Bogus b appare più contrastato, in media, del canale b vero. Questo è riscontrabile ad esempio nella parte color ciano della macchinina più o meno al centro della fotografia, ma non solo. Ciò dipende ancora una volta dalla cromaticità dei primari, ma anche dal gamut dello spazio RGB utilizzato: i canali che vedete provengono da un originale codificato in sRGB. Il gamut è quindi piuttosto ristretto, quindi a colori saturi corrispondono numeri elevati; anzi, alcuni dei colori nell’originale, come il rosso del tendone, sono molto vicini al clipping. Se convertiamo il file in uno spazio RGB a gamut più esteso, come ProPhoto RGB, i numeri cambieranno (saranno in generale più piccoli), ma l’aspetto dell’immagine no. Numeri più piccoli in gioco creano però canali Bogus meno contrastati. E questa è una delle differenze cruciali che possiamo riscontrare tra i canali Bogus e gli originali: conversioni diverse in Lab prodotte da originali RGB che differiscano soltanto per il profilo produrrebbero sempre gli stessi canali a e b, naturalmente nel momento in cui il diverso profilo RGB non modifichi il colore dell’originale. Questo non vale per i canali Bogus, e non deve sorprendere: il nostro finto Lab dipende da R, G e B, ovvero dallo specifico spazio in cui l’originale è codificato. Se cambiamo profilo, cambiano i numeri, e se cambiano i numeri cambiano anche i canali Bogus. I canali Bogus quindi imitano Lab, ma non codificano in maniera assoluta il colore.
Questo ci preoccupa? No. Il Bogus non è reale, è un’imitazione della realtà; della vita, se volete. E i R.E.M., nello splendido brano Imitation Of Life (se non avete mai visto il video, guardatelo – è uno dei capolavori assoluti del genere), cantano:
This lightning storm
This tidal wave
This avalanche, I’m not afraid.
Della tempesta di fulmini, dell’ondata di marea, della valanga – non abbiamo paura neppure noi: nel vero Lab abbiamo visto di peggio, credo. E ci sono anche un sacco di cose che non abbiamo visto e che non potremo vedere mai, se è chiaro il riferimento.
Così, questo articolo si chiude con una domanda irrisolta: già, ma a cosa serve tutto questo? Non voglio che questo scritto diventi lungo come un’enciclopedia e pertanto mi fermo qui, ma vi assicuro che serve. Abbiate pazienza fino al prossimo articolo e non resterete insoddisfatti. È una promessa.
Grazie per la vostra attenzione, messa stavolta a dura prova, e a presto!
MO
No, ci ho ripensato, aspettate un attimo…
E se in un momento di follia mi venisse voglia di definire un terzo canale non presente in Lab, qualcosa come
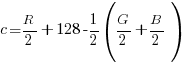
le cui componenti opponenti sono il ciano e il rosso, avrebbe senso, secondo voi? Che relazione c’è tra a, b e c se ne esiste una?


Non lo scarico….me lo voglio provare con calma appena ho occasione…..mi hai messo a pensare, ma molto…..
Quanto roba Marco!
E nemmeno è finita :-).
Ma era un articolo solo? Perche mi sembra d’averne letti quattro o cinque.
Mi hai lasciato senza parole, e non è la prima volta, tanto che sono fermo da alcuni minuti a pensare e non trovo un commento adeguato.
Chiarezza, passaggi logici e capacità investigativa sono gli aspetti che mi piacciono di più.
Grazie
Marco, ho riletto il tuo articolo fermandomi in particolare su un punto cruciale, quando dici: per R = G = B vogliamo avere a = 0 e b = 0. A commento del tuo precedente articolo, avendo come riferimento questo punto, ho proposto un modello che poi mi sono accorto essere difettoso. Ma ora, grazie a te, credo di aver trovato l’errore e vorrei riproportelo corretto, credo. Il modello serve solo a visualizzare il principio di base.
Nella retina, i tipi di coni sono tre e quindi, per quanto riguarda l’aspetto cromatico, il segnale luminoso viene scomposto nelle componenti RGB. In modo analogo funziona il sensore della fotocamera.
Ora, per come la vedo io, il problema è quello di trasferire le informazioni cromatiche RGB utilizzando 2 canali al posto di tre.
Per risolvere il problema prendo in prestito il tuo modello della bilancia, con qualche variazione. Anzi, le bilance sono 2, la bilancia a e la bilancia b. Entrambe hanno un braccio lungo il doppio dell’altro. Il braccio più lungo è quello che sorregge il piatto destinato alla misura dei pesi negativi (G la bilancia “a” e B la bilancia “b”). Il braccio più corto sorregge i pesi positivi (R+B la bilancia “a” e R+G la bilancia “b”. L’equilibrio si ottiene quando ad una quantità posta sul piatto negativo corrispondono due quantità sul piatto positivo.
In condizioni di equilibrio, quindi, i valori R, G e B corrispondono e si ha la neutralità.
La conversione avviene in questo modo:
Per prima cosa viene individuato il valore più basso e lo si sottrae a tutti e tre i valori misurati; in questo modo si elimina la componente grigia e si elimina anche un canale;
Seconda operazione: i due colori rimanenti vengono pesati in ogni piatto destinato a riceverlo, sia della bilancia “a”, sia della bilancia “b”.
Il risultato delle pesate determina il colore sia dei canali risultanti.
Prendo come prova il tuo primo esempio: Rosso: 255R0G0B si traduce in 128a128b
Prima operazione: non necessaria
Seconda operazione: R255 viene misurato nel piatto sorretto dal braccio corto della bilancia “a” e quindi la misura risulta dimezzata: quindi ottengo 128a.
Viene misurato anche nel piatto sorretto dal braccio corto della bilancia “b” e quindi la misura risulta dimezzata: quindi ottengo 128b.
Provo ora con il tuo quinto esempio: Magenta: 255R0G255B si traduce in 255a(128)b
Prima operazione: non necessaria
Seconda operazione: R255viene misurato come nell’esempio precedente e ottengo 128a e 128b.
Ma devo ancora misurare B255: viene misurato nel piatto sorretto dal braccio corto della bilancia “a” e quindi la misura risulta dimezzata: quindi ottengo 128a. Viene anche misurato nel piatto sorretto dal braccio lungo della bilancia “b” e quindi la misura risulta conservata: quindi ottengo (255). Sommando i valori ottenuti in a e in b ho il risultato di 255a e (128)b.
Stavolta mi pare che il modello funzioni.
Avevo pensato alla retina in quanto alcuni passaggi sono facili da pensare. Per esempio, il primo passaggio, dove viene sottratto il valore più basso. Poiché le informazioni inviate al cervello sono in sostanza dei segnali elettrici e, se non sbaglio, è essenzialmente la differenza di frequenza a determinare le caratteristiche del segnale, la frequenza più bassa di una tripletta di stimoli potrebbe funzionare da livello zero oltre il quale misurare gli altri segnali.
Ok, non vado oltre. Grazie per la pazienza. Ciao.
A occhio e croce mi sembra un ragionamento che funziona; è uno dei tanti modelli possibili, credo, sempre basato sulle analogie di cui scrivevo qualche tempo fa. In realtà proprio stasera, mentre scendevo in città per incontrare un vecchio amico, mi sono accorto che probabilmente nell’ultima domanda che ho sollevato (quella relativa all’utilità o meno di un possibile canale c) si nasconde qualcosa che non è del tutto evidente. Formulato in quel modo, il canale c dipende da a e b, quindi non è portatore di informazioni nuove e significative di per sé. Ma forse, scomponendolo, in una maniera strana, si potrebbe cavarne qualcosa che è più lungo da ricavare altrimenti. Se è così, però (ancora non lo so, devo provare), l’asimmetria dei due bracci della bilancia che tu proponi potrebbe avere una strana ricaduta. OK, è un puzzle: il tempo di mettere assieme i pezzi, ammesso che combacino, e poi vedo dove potrebbe andare a parare questa cosa. Grazie del commento!
Marco, è passato un po’ di tempo da quando hai scritto questo splendido articolo. Mi sono ritrovato a ragionare di nuovo sui canali a e b, quelli veri e quelli “falsi”. In particolare ho notato che nei verdi si ha una discreta differenza tra il vero b e quello falso. Quello vero è “più giallo”. Ho pensato alla vegetazione, a quei casi in cui c’è troppo giallo e ho provato a sostituire il vero b con quello falso, ottenendo in tal modo un certo miglioramento, ancora poco evidente ma mirato sui verdi. Ho quindi pensato, con calcoli, di mettere in differenza i due b, ottenendo in tal modo un canale alfa da contrastare con tono automatico e dal quale ricavare una maschera che, leggermente curvata, è piuttosto efficace nei verdi, specie quelli più saturi e gialli. Mi pare un buon modo per risolvere eventuali problemi cromatici della vegetazione con un intervento selettivo con le curve “a” o “b” di Lab.
Grazie ancora per tutti i tuoi scritti.
Da qualche tempo, (in realtà da poco) ho scoperto il tuo blog, e ho seguito con molto interesse alcuni tuoi post, tra cui anche questo sul falso Lab partendo da RGB, veramente interessante per creare delle basi per delle maschere in modo veloce.
Questo mi ha fatto riflettere sulla possibilità di avere in Lab oltre ai canali “a” e “b” anche un terzo canale, diciamo “c” che rappresenti l’asse degli opponenti Ciano Rosso.
E perché non un canale diciamo “d” perpendicolare al precedente che rappresenta l’asse Viola Lime. si avrebbero così 4 canali utili, i due normali + altri due, oltre ovviamente al canale L.
Io sono un Artista illustratore che utilizza la fotografia e ho una pratica di Photoshop maturata negli anni, ma ho una conoscenza piuttosto basica della matematica, perciò ho seguito con fatica le formule che proponi.
Però mi piace sperimentare e ho pensato che tra i metodi di fusione che come dici sono degli operatori avrei potuto trovare una soluzione. Alla fine sommando e sottraendo opportunamente tra loro i canali a e b del Lab ho ottenuto quello che cercavo (o almeno credo).
In una mattinata di sperimentazione sono arrivato a costruire un azione che mi crea i due canali in questione.
Ovviamente vorrei un tuo parere per capire se ho preso un granchio e se ci sono delle falle nel ragionamento, anche perché la procedura come l’ho sviluppata è piuttosto semplice e banale.
In pratica,:
– per ottenere il canale “c” (asse Ciano-Rosso con Ciano -127 e Rosso 127) duplico “a” , poi Applica Immagine, add “b” ofsett -128
– per ottenere il canale “d” (asse Viola-Lime con Viola -127 e Lime 127) duplico “b” , poi Applica Immagine, sottrai “a” ofsett +128.
In questo modo mi sembra che tutto funzioni, i neutri rimangono tali.
I canali che si ottengono sono comunque interessanti per un uso come maschere.
Sergio, grazie dell’interessante osservazione. Purtroppo non ho Photoshop davanti e quindi ti rispondo cercando di fare i conti a memoria. In linea teorica è corretto, ma credo che bisogna stare attenti. Abbiamo dei numeri a 8 bit, codificati in modo che siano compresi tra -128 e +127. Se li sommiamo, l’intervallo teorico di variabilità è compreso tra -256 e +254, perché ci servono 9 bit in totale. Questo può causare clipping e comportamenti strani: pertanto io prima dividerei i numeri del primo canale per 2. Il modo più immediato è curvare il canale duplicato in modo che il contrasto si dimezzi. Poi aggiungerei il canale restante, ma non con l’offset: utilizzerei Scala = 2, per dividere anche quello. In questo modo a occhio rimani all’interno dell’intervallo, perché il caso peggiore (-128 in entrambi i canali) diventa: -64 + (-128 / 2) = -64 – 64 = -128. Magari domani cerco di provare appena ho Photoshop sottomano, ma a occhio mi sembra corretto così.
Uscendo da Lab (o, meglio, rimanendo in RGB), c’è un metodo interessante in questo articolo di Luca Negri che ne ha scritto poco tempo fa. Forse vale la pena di dare un’occhiata…
Grazie ancora, a presto!
MO