Una nuova caTEgORIA
Questo articolo, oltre che il 2013, inaugura una nuova categoria in questo blog: l’ho denominata Teoria. Non spaventatevi: gli articoli teorici non tratteranno di cose eccessivamente astruse. Il loro scopo è solo quello di suggerire in maniera spero intuitiva alcuni concetti di base, talvolta mediante paragoni e modelli non del tutto canonici. In particolare, lo scopo di questo articolo è mettere in evidenza alcuni parallelismi tra i metodi colore e altre strutture matematiche di facile comprensione, in modo da suggerire dei possibili punti in comune tra mondi apparentemente scollegati. Inoltre vorrei introdurre un modello tratto dalla fisica per illustrare una delle caratteristiche più sfuggenti del metodo colore Lab. Insomma, come avrete capito stavolta la prendo larga: anzi, larghissima.
L’importanza del sistema di riferimento
Chiunque abbia studiato un po’ di matematica sa cos’è un sistema di riferimento. Si tratta di un sistema di coordinate (numeri, in parole povere) che si utilizza di norma per individuare la posizione di un punto nello spazio. Non esiste uno solo sistema di riferimento, ma infiniti – e le loro caratteristiche dipendono da come sono definiti. Inoltre, esistono diverse categorie di sistemi di riferimento possibili. Facciamo un esempio.
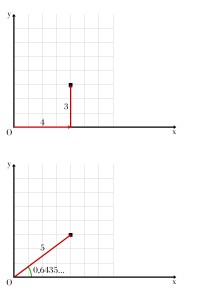
Quello che vedete nell’immagine qui a fianco, sopra, è un possibile sistema di riferimento in due dimensioni. Per definirlo non serve molto: bastano due assi, chiamati x e y, un punto in cui si intersecano (detto origine e indicato con la lettera O), un’unità di misura per ciascun asse e magari anche l’angolo formato dagli assi stessi, che di solito è retto – benché questa non sia una prescrizione assoluta. Se l’angolo formato dagli assi è retto il sistema di riferimento viene definito ortogonale. In una certa posizione del piano ho segnato un punto. Le indicazioni per arrivarci partendo dall’origine sono semplicissime: muoviti lungo l’asse x di quattro unità, e poi di tre unità lungo l’asse y. Detto, fatto. Sotto, vediamo rappresentato lo stesso punto, ma ci accorgiamo che possiamo arrivarci anche in un altro modo: possiamo pensare di tracciare una retta che congiunga l’origine con esso e percorrerla fino a che non arriviamo a destinazione. Ci servono nuovamente due numeri: la distanza che dobbiamo percorrere e l’angolo formato dalla retta con uno degli assi; diciamo l’asse x, per comodità. Naturalmente avremo stabilito anche un’unità di misura – in pratica, quanto sono lunghi i nostri passi mentre ci dirigiamo verso il punto.
Si tratta evidentemente di due sistemi di riferimento diversi. Il primo prende il nome di sistema cartesiano, il secondo di sistema polare. Le coordinate che usiamo per identificare il punto sono nel primo caso (4, 3), dove per convenzione il primo numero indica x e il secondo y; nel secondo caso (5, 0,6435…), dove per convenzione il primo numero indica la distanza dall’origine e il secondo l’angolo formato con l’asse x dalla retta lungo cui ci muoviamo (espresso in un’unità di misura che prende il nome di radiante). In coordinate polari, il primo numero è simbolicamente indicato con r, il secondo con θ, ovvero la lettera greca theta. È palese che le coppie di numeri (x, y) e (r, θ) non sono uguali: eppure rappresentano il medesimo punto, una volta che diamo loro la giusta interpretazione. Se, ad esempio, utilizzassimo la seconda coppia di numeri come se fossero coordinate cartesiane nel sistema disegnato nella figura, arriveremmo certamente in un punto – ma sarebbe diverso da quello disegnato nel piano nella figura: si troverebbe 5 caselle verso destra e 0,6345… caselle verso l’alto.
Cartesio in Photoshop
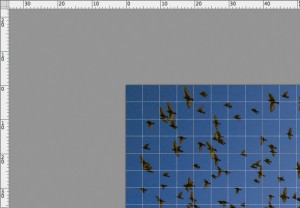
Gli assi cartesiani si trovano letteralmente ovunque: quando visualizzate i righelli e la griglia in Photoshop non fate altro che attivare la visualizzazione di due distinti sistemi di coordinate cartesiane. Nei righelli ci sono gli assi, orizzontale e verticale; c’è l’origine, che in assenza di altre istruzioni viene fatta coincidere con l’angolo in alto a sinistra del documento ed è individuabile tramite i due numeri 0 che compaiono, uno per asse; c’è l’unità di misura, che può essere modificata. L’origine può essere spostata: è sufficiente cliccare con il mouse all’incrocio dei righelli e trascinare il mouse all’interno della finestra, mantenendo premuto il tasto, fino a che il puntatore non si trova nel punto che desideriamo impostare come nuova origine.
La griglia è invece un sistema cartesiano più implicito, per così dire, che può sembrare connesso ai righelli ma gode in realtà di una sua indipendenza. Nell’immagine riportata qui sopra, l’unità di misura dei righelli è il millimetro. I numeri dipendono dalla dimensione in pixel del documento e dalla sua risoluzione: se modificate la dimensione dell’immagine senza ricampionarla, vedrete che i numeri nei righelli variano. La griglia invece è impostata in modo che le righe cadano ogni 2 centimetri, e che ci siano quattro suddivisioni per ogni quadrato che si forma in questo modo. Per inciso, le proprietà di righelli e griglia si possono impostare nelle preferenze di Photoshop, rispettivamente nelle sezioni “Unità di misura e righelli” e “Griglie, guide e sezioni”.
La realtà e le sue rappresentazioni
Il bello dei sistemi di riferimento è che possiamo utilizzare il sistema che preferiamo per descrivere la posizione di un punto, perché varieranno i valori ma non la sostanza di ciò che descriviamo. In altri termini, varierà la rappresentazione della realtà, ma non la realtà. Inoltre possiamo scegliere di utilizzare questo o quel sistema di riferimento a seconda di quale ci risulta più comodo. Ma cosa significa “più comodo”?
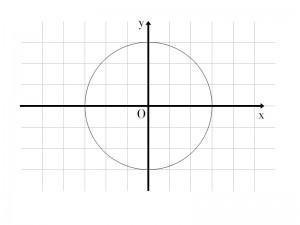
Osserviamo la circonferenza nella figura a fianco. Non è una forma geometrica particolarmente complicata, ma la sua espressione formale è assai diversa a seconda che decidiamo di utilizzare le coordinate cartesiane o le coordinate polari. Nel primo caso, possiamo affermare che la circonferenza (che, come potete notare, ha un raggio pari a 3 unità) soddisfa questa equazione:
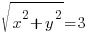
oppure, in forma equivalente:
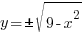
Questo è sufficiente, di solito, per mandare in crisi un buon numero di persone. Ma se date un’occhiata allo schema delle coordinate polari riportato sopra, vi accorgerete che per generare una circonferenza è sufficiente far ruotare il suo raggio attorno all’origine di 360° o, se preferite, di 2π radianti (sono due unità di misura diverse, ma l’angolo è lo stesso): l’unico parametro importante è, per l’appunto, il raggio stesso. In questo modo, la circonferenza che ho tracciato è esprimibile in coordinate polari in questo modo:
Questa è una notazione compatta, semplice e comprensibile che ci causa molti meno mali di testa rispetto alle formule espresse in coordinate cartesiane. Ricordo ancora che entrambe le rappresentazioni sono corrette: scegliere l’una o l’altra è solo una questione di comodità. Perlomeno: lo è oggi. Giordano Bruno e Galileo Galilei pagarono un prezzo enorme semplicemente per aver osato sostenere che il modello eliocentrico, che poneva il sole al centro del sistema solare, fosse una rappresentazione migliore di quello geocentrico, il quale rendeva estremamente complicato calcolare le orbite dei pianeti ma aveva il vantaggio di porre la Terra (e quindi, l’essere umano) al centro dell’universo. In ogni caso, se decidete per vostra comodità di leggere i colori in Lab quando in realtà state lavorando in RGB o CMYK, oggi, non dovreste finire al rogo. (Forse.)
Da Cartesio ai metodi colore

Tutto questo ha ovviamente una connessione con ciò che ci interessa di più – ovvero il colore. Osservate queste sequenze di coordinate cromatiche: 63R84G143B; 90C70M15Y0K; 35L4a(39)b; 225H56S56B. Dopo avere ricordato che la parentesi nella terza formula rappresenta un numero negativo, chiedo: cos’hanno in comune? Apparentemente nulla, ma in realtà rappresentano lo stesso colore, che potete vedere qui a fianco. Non ho usato il verbo “rappresentano” in maniera generica: le coordinate che avete appena visto sono rappresentazioni diverse dello stesso “oggetto”, rispettivamente in RGB, CMYK, Lab e HSB. Volendo, potrei aggiungere altri metodi colore a questi quattro. Naturalmente, le coordinate in questone rappresentano lo stesso colore se le impostazioni che usate sono identiche alle mie, altrimenti i numeri sarebbero diversi. Ovvero, la mia affermazione è vera se in Photoshop RGB è impostato su Adobe RGB e se CMYK è impostato sul profilo standard Coated FOGRA39. I valori HSB, per inciso, dipendono dalle impostazioni di RGB. Quindi, anche qui: stessa realtà, rappresentazioni diverse.
Il fatto che le coordinate cartesiane necessitino della definizione di una scala, ovvero di un intervallo base che nell’immagine vista poco sopra è rappresentato dal lato dei quadretti che costituiscono la griglia, ha una curiosa ricaduta anche nel mondo del colore. Se avessimo definito l’intervallo base diversamente, ad esempio pari al 75% dell’intervallo che abbiamo utilizzato, la griglia sarebbe stata diversa: in questo caso, più fitta. Le coordinate del punto rappresentato non sarebbero state (4, 3) bensì (5,333…, 4): avremmo avuto bisogno di più passi per arrivare nello stesso punto. Non vi sembra simile ai profili colore? Pensate a due varianti di RGB: lo stesso colore (in questo modello, lo stesso punto) è rappresentato da terne differenti, ad esempio, in sRGB e Adobe RGB. In realtà sto barando: non è sufficiente affermare che tra queste due varianti del metodo colore RGB la scala è diversa per spiegarne le differenze, in quanto sono diverse anche le cromaticità (ovvero, in parole povere, i valori dei colori primari) ma credo che questo possa almeno suggerire intuitivamente parte della differenza.
In tre dimensioni, il gamut
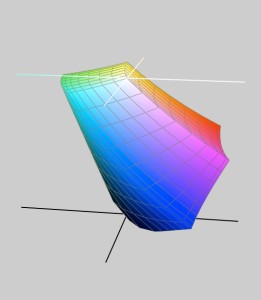
Nella figura a fianco abbiamo fatto un passo in avanti: si tratta della rappresentazione tridimensionale (in realtà, una proiezione bidimensionale di un “volume”) del cosiddetto gamut di uno spazio colore – in questo caso sRGB. Gli assi non sono due, ma tre: uno è nascosto e attraversa verticalmente tutto il volume rappresentato. Il terzo asse attraversa l’intersezione degli assi disegnati in nero e quella degli assi disegnati in bianco. Quell’asse rappresenta la chiarezza, ovvero la coordinata L di Lab: più saliamo, più chiaro ci appare il colore. Gli altri due assi identificano i canali a e b: a (verde-magenta) è identificato dall’asse che ci appare trasversale, b (blu-giallo) da quello che sembra puntare verso di noi. Il gamut (o, meglio, una delle possibili rappresentazioni del gamut) altro non è che un volume in uno strano spazio cartesiano in cui gli assi non misurano distanze fisiche, ma hanno i valori delle tre coordinate base del metodo Lab. Nulla ci impedirebbe di utilizzare R, G e B per indicare i tre assi, ma il grosso vantaggio di utilizzare L, a e b consiste nel fatto che tali coordinate siano assolute: i loro valori non dipendono da profili vari, a differenza di quanto accade in RGB. Quindi, questa è una delle rappresentazioni più diffuse per mostrare il gamut di un certo spazio colore. Che, ricordatelo, è tridimensionale: dovete pensare al bizzarro volume rappresentato in figura come qualcosa che potete ruotare ed esaminare da ogni lato. Su Macintosh, lanciando l’utility denominata ColorSync, potete facilmente rendervi conto di questa tridimensionalità.
La rappresentazione e il modello
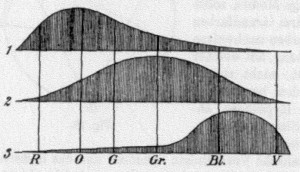
Facciamo un passo avanti: dietro ogni rappresentazione c’è un modello, naturalmente, che si spera abbia almeno qualcosa a che vedere con la realtà dei fenomeni che descrive. Questa richiesta però non è sempre necessaria. Ad esempio, RGB si basa sui fenomeni che si verificano quando si esamina il comportamento degli illuminanti; CMYK si basa invece sul comportamento di inchiostri e pigmenti. Ma Lab cosa rappresenta? Questo si può spiegare abbastanza facilmente, e chi è venuto ai miei corsi lo sa. Riassumendo, il modo migliore per comprendere la genesi del metodo Lab è risalire alla disputa tra Hermann von Helmholtz ed Ewald Hering. Quest’ultimo era un fisiologo che nel 1892 propose la sua teoria dei colori opponenti, che criticava la teoria tricromatica elaborata da Thomas Young e von Helmholtz. La teoria tricromatica propone un modello basato essenzialmente sull’ipotesi (poi verificata come corretta) che il nostro occhio contenga tre tipi di sensori per il colore. Un essere umano normale è dotato di tre tipi di cellule fotosensibili denominate coni (identificate dalle lettere L, M e S), che reagiscono principalmente (ma non esclusivamente) a stimoli luminosi di tre lunghezze d’onda diverse che possiamo identificare in maniera abbastanza vaga con i colori rosso, verde e blu. (Attenzione: un ipotetico metodo colore LMS non coincide con RGB: anzi, nel 2006 Judah B. De Paula ha proposto una formula di conversione da un metodo all’altro.)

Hering sosteneva invece che la nostra percezione del colore può essere spiegata da tre processi opponenti, identificabili come chiaro-scuro, rosso-verde e giallo-blu, e che la teoria tricromatica non consente di spiegare certi fenomeni che invece il suo modello rende molto semplici da comprendere. Parliamo di colori opponenti, in questo contesto, perché il bianco e il nero, così come gli elementi delle coppie rosso-verde e giallo-blu non possono essere percepiti allo stesso tempo all’interno di un singolo stimolo. In parole povere, un oggetto chiaro non può essere al contempo scuro, così come un oggetto rosso non può essere al contempo verde, e un oggetto giallo non può essere anche blu. Altri colori possono venire sintetizzati a partire dai quattro appena citati: un arancione, ad esempio, è un rosso contenente del giallo, ed è possibile immaginare un arancione più virato verso il rosso o verso il giallo. In RGB costruiamo invece il giallo con il rosso e con il verde, ma non per questo percepiamo il rosso e il verde come entità separate: e il concetto di “rosso verdastro”, così come quello di “giallo bluastro” non ha alcun senso per noi. Non riusciamo a immaginare colori di questo tipo. In realtà la questione è ancora dibattuta, anche perché il meccanismo dei processi opponenti non ha ancora una spiegazione scientifica rigorosa. Per inciso, nel 1983 due ricercatori di nome Hewitt D. Crane e Thomas P. Piantanida realizzarono un esperimento in cui alcuni osservatori affermarono di poter vedere questi “colori impossibili”, ma non c’è ancora alcuna certezza su questo fatto. A margine: nell’immagine riportata sopra, tratta da Wikipedia, c’è un piccolo errore concettuale. Riuscite a vederlo?
A prescindere da questo: chi aveva ragione? Von Helmholtz o Hering? Per strano che possa sembrare, avevano ragione entrambi. Il modello tricromatico è corretto a livello di registrazione dello stimolo, all’interno dell’occhio. Le cellule fotosensibili, però, inviano i loro segnali elettrici al cervello attraverso il nervo ottico, e nel percorso i segnali sembrano ricombinarsi in maniera tale da giungere a destinazione in una forma che non ha più granché a che vedere con le componenti R, G, B originali. Arrivano, in sostanza, un segnale di luminosità e due segnali puramente cromatici, non si sa ancora bene in base a quale meccanismo, che sembrano abbastanza ben imitati dalle tre componenti del sistema Lab.
Una difficoltà concettuale
Nel corso delle classi da me tenute ho notato che il concetto appena esposto viene compreso da chiunque senza difficoltà. Quello che sfugge, probabilmente perché richiede un salto concettuale notevole, è il dualismo intrinseco dei colori primari di Lab. Credo che se a questo punto chiedessi a qualcuno che si trovasse a leggere queste idee per la prima volta quanti siano i colori primari di Lab, risponderebbe “quattro”. Ed elencherebbe il verde, il magenta (che nel modello di Hering è rosso), il blu e il giallo. Questo è un errore: i primari (cromatici) di Lab sono solo due e in essi le tinte vivono accoppiate. Si tratta del primario verde-magenta e del primario blu-giallo, che tutti qui riconoscerete come legati ai canali a e b, rispettivamente. In più abbiamo il canale L, che codifica solo la luminosità (meglio: chiarezza) dello stimolo, indipendentemente dal colore.
Il vecchio modello della bilancia

So per esperienza che questo concetto è evanescente e da tempo cerco un modello che lo renda comprensibile. Ho avuto feedback positivi sul modello che presento nel mio videocorso sul metodo Lab realizzato per Teacher-in-a-Box: il modello si basa su una bilancia a due piatti, che pende da una parte o dall’altra a seconda del peso che mettiamo su ciascun piatto. Nel canale b, ad esempio, abbiamo un piatto del blu e un piatto del giallo, e l’equilibrio – ovvero la neutralità – si ottiene quando la bilancia non pende da nessuna parte. Convenzionalmente consideriamo negativi i pesi che spostano la lancetta verso sinistra (ovvero i colori più blu che gialli, b < 0) e positivi quelli che spostano la lancetta verso destra (i colori più gialli che blu, b > 0). Un aspetto sottile di questo modello è che questo genere di bilancia può solo funzionare con due piatti: appena ne togliamo uno, l’altro crolla e di fatto la bilancia non esiste più come tale. In altri termini, una sorta di equilibrio tra le due componenti (i due piatti) è necessaria, e la non-separabilità delle stesse è in qualche modo sottintesa da questo fatto. Di recente ho però pensato a un nuovo modello, forse più originale, che espongo nel seguito e che descrive a mio modo di vedere molto bene quale sia il legame indissolubile tra le componenti opponenti di a e b.
Ci serve una calamita (ma prima, ci serve un po’ di fisica)
Grazie al mio trascorso di fisico, credo molto nelle analogie. Analogia, per me, significa prendere un concetto che può anche essere totalmente scollegato da ciò che stiamo esaminando e vedere se esista un qualche parallelismo in grado di gettare luce su un’idea poco chiara grazie a qualcosa di più facilmente comprensibile. Per questo oggi parlerò di particelle elementari.

Per poca fisica che conosciate, avete tutti almeno vagamente sentore del fatto che alcune particelle sono dotate di carica elettrica. A livello di componenti atomici, l’elettrone ha carica negativa, mentre il protone (uno dei componenti del nucleo atomico) ha numericamente la stessa carica, ma di segno positivo. Altre particelle (come il neutrone, un altro “mattone” del nucleo) hanno carica zero. Per una particella, possedere una carica elettrica implica due cose: primo, essere in grado di generare un’entità che chiamiamo campo elettrico; secondo, essere in grado di reagire alla presenza di un campo elettrico generato da una o più cariche diverse. Una particella neutra, ovvero a carica zero, non genera alcun campo elettrico e rimane indifferente a eventuali campi presenti nella regione spaziale in cui si trova. Ciò che differenzia il comportamento tra particelle cariche negativamente, come l’elettrone, e positivamente, come il protone, è che la loro reazione allo stesso campo elettrico è esattamente opposta. Inoltre, particelle dotate della stessa carica elettrica si respingono mentre particelle di carica opposta si attraggono secondo una legge molto simile, formalmente, a quella che regola l’interazione gravitazionale, ma con una differenza sostanziale: la gravitazione è sempre una forza attrattiva, e non esiste una repulsione gravitazionale. Non c’è, insomma, una “carica di gravità”, ma una massa che è sempre positiva. E due masse si attraggono, inesorabilmente. Questo è, in estrema sintesi, il riassunto dei fenomeni elementari dell’elettrostatica.
Quando le cariche si mettono in moto

Oltre all’interazione elettrostatica esiste anche un’interazione magnetica. Questa di nuovo si fa risalire alle cariche elettriche, e la cosa sorprendente è che elettricità e magnetismo, due fenomeni che sembrano totalmente scorrelati tra loro, sono due facce della stessa medaglia. Questo fatto fu sancito da James Clerk Maxwell nel diciannovesimo secolo con il famoso insieme di equazioni che porta il suo nome, e il tutto si può riassumere, iper-semplificando, come segue: se osserviamo una carica elettrica ferma rispetto a noi, misuriamo un campo elettrico; non appena questa carica elettrica si muove, misuriamo un campo magnetico. Ma se ci stessimo muovendo assieme a questa carica, se ci fossimo in qualche modo seduti sopra, non misureremmo alcuna forma di magnetismo dovuta al suo moto. Questo fatto ha ramificazioni così formidabili e profonde che all’inizio del XX secolo ebbe ripercussioni su teorie nuove e complesse, talvolta in contraddizione con la nostra esperienza comune. Ad esempio, la teoria della relatività speciale formulata da Albert Einstein.
Quello che ci importa in questo contesto è però diverso. Se, come abbiamo detto, il campo elettrico è generato dalle particelle cariche, possiamo dire la stessa cosa anche del campo magnetico? Posta in questo modo, la domanda è ambigua. Sì, nel senso che il campo magnetico è generato da particelle cariche in movimento rispetto all’osservatore. Allo stesso tempo, però, esistono delle entità che generano un campo magentico (pensate a una semplice calamita, o anche al nostro pianeta, che si comporta come una gigantesca calamita in questo senso), ma non esistono cariche magnetiche simili alle cariche elettriche: ovvero, non esistono cariche magnetiche negative separate e distinte da cariche magnetiche positive. Perlomeno, non sono state ancora trovate, anche se potrebbero esistere in teoria almeno in linea di principio. I generatori del campo magnetico vivono sempre accoppiati, per amore o per forza, in forma di entità dette “dipoli” (con l’accento sulla “o”), che si contrappongono ai “monopoli” elettrici come gli elettroni o i protoni descritti poco fa.
I dipoli non si spezzano
Possiamo pensare di prendere una calamita, dotata di due poli (che vengono convenzionalmente denominati Nord (N) e Sud (S)) e spegnere uno solo di essi? No: se spezziamo una calamita in due pezzi non ci ritroviamo con due frammenti caratterizzati da una carica magentica isolata (N o S), bensì con due calamite più piccole, ciascuna con i suoi identici poli N e S. Intendo: entrambi i poli insieme. E così avanti, di suddivisione in suddivisione, fino ad arrivare alle più piccole componenti subatomiche. Il monopolo magnetico, ammesso che esista, sfugge e non vuole saperne di manifestarsi.
Che c’entra tutto questo con il colore? C’entra, a livello di modello. I primari di RGB sono come le cariche elettriche: R può esistere da solo, G può esistere da solo, B può esistere da solo. Ma i primari di Lab hanno due poli ciascuno: non esiste “il verde” in Lab, così come non esiste “il magenta”. Esiste un verde-magenta, incarnato dal canale a. E non possiamo separare i due poli: un primario di Lab è un dipolo cromatico, se vogliamo chiamarlo in questo modo. È il linguaggio che usiamo che spesso diventa scivoloso e ci trae in inganno: quando diciamo “verde” o “magenta” riferendoci a un canale a negativo o positivo, rispettivamente, commettiamo un’imprecisione linguistica oltre che concettuale. Un valore negativo in a è “più verde di quanto non sia magenta”, e un valore positivo è “più magenta di quanto non sia verde”. Se non pronunciamo la formula completa e usiamo le abbreviazioni “verde” e “magenta” è semplicemente per non impazzire, ma dobbiamo sempre tenere presente il concetto di fondo: i primari di Lab sono formati da colori opponenti, come il polo N e il polo S di un magnete, che non possiamo separare.
La neutralità nell’occhio dei ciclone
Spesso l’espressione “essere nell’occhio del ciclone” viene utilizzata in maniera impropria: con questa frase si indica una situazione di grave pericolo, stress o comunque difficoltà, mentre in natura è il contrario. Nell’occhio, ovvero nel centro di un ciclone c’è spesso calma assoluta (ma attenzione, è in arrivo il lato B del ciclone stesso…). Perché sto usando questo paragone? Pensate al colore grigio: un colore neutro, acromatico, ovvero privo di tinta, che non può virare verso nulla. Non è né verde né magenta, né blu né giallo – vive (in ciascuno dei due canali a e b di Lab) esattamente nel centro di due tensioni che sono quelle dei colori opponenti. In questo senso è in quiete quanto un corpo soggetto a due forze contrapposte di uguale intensità: non si muove nulla, ma appena una delle due forze si manifesta il corpo si muove in quella direzione. Comprendete dunque che la codifica standard dei canali a e b di Lab è molto sensata: assegniamo il valore 0 a ciò che si trova nel mezzo, numeri negativi a una delle due forze contrapposte (il polo “freddo” del dipolo cromatico) e numeri positivi all’altra (il polo “caldo”). La regola: colori freddi, segno meno; colori caldi, segno più. In a, numeri negativi indicano uno spostamento verso il verde; in b, verso il blu. Viceversa, numeri positivi indicano uno spostamento verso il magenta in a, verso il giallo in b.
L’origine cade dove vogliamo noi
La rappresentazione di questi numeri richiede però un discorso diverso. I canali, vi ricordo, sono immagini in scala di grigio, che possono andare solo dal nero al bianco. Abbiamo appena detto che vogliamo assegnare il valore 0 al punto neutro che vive a metà dei due canali a e b. Se però rappresentiamo la loro luminosità con valori che vanno da 0 a 255, come se fossero RGB, è impossibile assegnare il valore 0 al colore “né verde, né magenta” o “né blu, né giallo”. Ovvero, abbiamo un problema quando vogliamo rappresentare visivamente il canale: in un’immagine in scala di grigio non esiste una luminosità corrispondente a un qualsiasi numero negativo: al minimo valore ammesso abbiamo il nero, in corrispondenza dello 0, il bianco in corrispondenza di 255. Ma nel modello che abbiamo costruito, i numeri negativi esistono e denotano uno spostamento verso le tinte fredde. Come possiamo fare? L’unica cosa sensata da fare è assegnare un valore di luminosità RGB medio al punto neutro del canale. Questo spiega perché la rappresentazione in scala di grigio dei canali a e b in Lab assegna il grigio al 50% (che ha luminosità pari a 128 in RGB) a un numero che in realtà chiamiamo 0; assegna il nero (che ha luminosità pari a 0) a -128; e infine il bianco (luminosità: 255) a 127. Insomma: i due sistemi di riferimento hanno la stessa scala, ma origini diverse. Questo tende a confondere le idee, ma bisogna sempre ricordare: sono rappresentazioni diverse della stessa realtà. Due sistemi di riferimento omogenei ma distinti.
Il significato dei numeri

Facciamo un esempio pratico osservando la serie di campioni qui a fianco. Si tratta di sette diversi colori caratterizzati da luminosità costante (L non varia, è sempre pari a 50), a costante (è sempre pari a 0) e b variabile. Dall’alto verso il basso, e ricordando che le parentesi indicano valori negativi, i valori di b sono: (40), (20), (10), 0, 10, 20, 40. Si vedono un sacco di cose istruttive in questa innocua serie di tacche colorate. La prima è che certamente percepite i colori estremi come più chiari degli altri. Questo è dovuto a un effetto, noto come Effetto Helmholtz-Kohlrausch, che in sostanza osserva come la nostra percezione della chiarezza (luminosità) di uno stimolo vari al variare della saturazione dello stesso. Più un colore è saturo, più ci appare luminoso, almeno entro certi limiti. È un effetto ancora misterioso e poco compreso, e se siete interessati potete trovare un’analisi più approfondita dello stesso nel mio articolo dedicato a esso nella documentazione del pannello PPW di Dan Margulis, che potete scaricare qui (in italiano) o qui (in inglese). La seconda è che i colori non vi sembrano uniformi: sembrano esserci dei leggeri gradienti all’interno dei singoli rettangoli. Vi assicuro che non è così, e potete convincervene scaricando l’immagine e misurandone le aree con il pannello Info in Photoshop. Quello che state guardando in faccia è il fenomeno del contrasto simultaneo: se osservate, ad esempio, il secondo rettangolo dall’alto, che corrisponde al colore 50L0a(20)b, appare più blu nella parte bassa di quanto non sia in quella superiore. In realtà è identico: non è più blu, ma appare più blu perché il rettangolo sopra di esso ha un blu più intenso di quello che si trova sotto. Se vogliamo, in termini di colori opponenti, quello che si trova sotto è meno blu, ovvero più giallo. Il nostro occhio se ne accorge e mette in atto lo straordinario fenomeno che ci permette di percepire i colori diversamente rispetto a ciò che li circonda: qualcosa che uno spettrofotometro non è in grado di fare. Tutto questo non è affatto di interesse solo accademico: in un’immagine reale, percepiremmo un blu come quello che stiamo esaminando in maniera molto diversa, a seconda che lo sfondo sia più blu o meno blu di esso. Lo stesso vale per il rettangolo centrale: è rigorosamente neutro (50L0a0b) ma ci appare più giallo sopra e più blu sotto. A questo punto dovreste essere perfettamente in grado di comprendere perché.
Numeri un po’ confusi
Una cosa che spesso risulta poco chiara nella definizione del metodo Lab è la scala utilizzata per L, che peraltro ha un suo senso preciso. L è la chiarezza, ovvero un attributo percettivo relativo del colore. È relativo perché esprime la brillanza di uno stimolo relativamente a quella del bianco, e la brillanza è collegata a una grandezza fotometrica (non percettiva, quindi) denominata luminanza. Il problema è che questa scala va da 0 a 100, dove 0 rappresenta la minima chiarezza possibile e 100 la massima. Il criterio quindi è simile a quello di RGB: numeri bassi, colore scuro; numeri elevati, colore chiaro. La scala numerica, però, è quella di CMYK, ma invertita: in CMYK, 0% significa assenza d’inchiostro, quindi la percezione di qualcosa di chiaro (il bianco della carta, tipicamente), mentre 100% significa massima densità d’inchiostro: non necessariamente “scuro”, visto che l’inchiostro giallo, ad esempio, è molto luminoso e brillante, ma certamente più scuro di 0%. Una gran confusione, quindi: L ha i valori orientati come RGB ma la scala (numerica: i valori Lab non indicano percentuali) di CMYK, e questo ha confuso più di uno studente. In realtà, se la scala di L fosse graduata da 0 a 255, si rischierebbe comunque di fare confusione con RGB, e potenzialmente tutto sarebbe ancora meno chiaro. In ogni caso, così è e così dobbiamo tenercela, ma ricordate che quel valore pari a 100 non ha assolutamente nulla a che fare con CMYK.
Conclusioni
E siamo giunti al termine di questa lunga panoramica, il cui scopo era quello di chiarire due cose.
La prima: i numeri che attribuiamo ai colori in qualsiasi metodo colore non sono altro che coordinate in uno strano spazio che non misura distanze ma valori cromatici. Al punto che, in colorimetria, si defìnisce perfino la distanza tra due colori. Se due colori sono caratterizzati dalle terne (L1, a1, b1) e (L2, a2, b2), la loro “distanza” è espressa da questa formula:
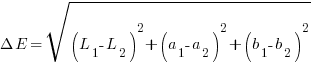
La prima lettera che compare nell’espressione è una lettera greca: delta (maiuscola), che in matematica quasi invariabilmente denota una differenza. Se i due colori sono uguali, ovvero le due terne sono identiche, la distanza tra loro è pari a 0. Chiunque abbia un minimo di dimestichezza con la geometria analitica ha certamente riconosciuto la formula della distanza tra due punti di uno spazio cartesiano tridimensionale. E questo parametro (o, meglio, la media di una serie di parametri calcolati su un certo numero di colori di riferimento) è esattamente quello che vi fornisce l’indice della bontà statistica del profilo del vostro monitor o della vostra stampante, ad esempio: vengono calcolati i ΔE tra i campioni originali di riferimento e quelli effettivamente restituiti dal vostro dispositivo, e quindi mediati. Attenzione che si tratta comunque di un valore statistico: potreste avere, almeno in linea di principio, una discrepanza molto forte in un certo colore e dei valori molto piccoli su tutti gli altri. In questo caso la media sarebbe piccola, e indicherebbe una buona corrispondenza, ma certi colori potrebbero essere fortemente falsati.
La seconda: delineare un’analogia un po’ stravagante per spiegare che i primari cromatici dello spazio Lab sono due, non quattro come si potrebbe credere. Il modello magnetico, che ruota attorno al concetto di dipolo, è molto simile a quello dei canali Lab – perlomeno nella mia testa: due forze opposte che non sono separabili e che generano quindi una situazione completamente diversa rispetto a quella in cui i primari sono definiti tramite cromaticità individuali, come nel modello RGB.
Come sempre, grazie per l’attenzione e alla prossima!
MO


6 Unico…Articolo stupendo…
Grazie Mattia, ma… è solo una questione di sistema di riferimento. Se ci si sforza di pensare lungo traiettorie un po’ diverse da quelle canoniche a volte viene qualche idea (a volte, invece, è meglio andare a dormire). Tutto qui!
Avrei dovuto gustare questo articolo con un tumbler basso di whiskey d’annata e un buon sigaro cubano, magari davanti al fuoco mentre fuori cade la neve.
Peccato che questo contorno sia mancato totalmente, avrebbe valorizzato degnamente questa splendida lettura.
Grazie Tiz! In realtà il merito è di mio figlio. A inizio dicembre stavamo giocando con dei legnetti magnetici, e lui ha notato che da una parte si attraevano e dall’altra parte si respingevano. E mi ha chiesto: “se li spezziamo in due, cosa fanno?” Buona domanda, mi sembra. Mentre gli spiegavo che avremmo ottenuto due calamite uguali, come si può spiegarlo a un bimbo di quattro anni, mi è venuta in mente l’idea del dipolo per il Lab. Ne ho parlato con Marco Diodato prima di Natale, e mi ha detto la stessa frase che tu avevi detto su Doris Franceschini :-). Quindi ho pensato che forse l’idea non era da buttare via.
Ho scritto il grosso a casa, sull’iPad, prima di dormire nelle sere festive. E no, non avevo bevuto whiskey neanch’io – anche se potrebbe sembrare…
Interessante, chiaro e scientifico, grazie Marco! Una riflessione a margine: mi sono sempre chiesto come mai “artefatti” digitali come la maschera di contrasto fossero accettati e in certa misura “graditi” alla nostra percezione. Possibile che siano interpretati come una naturale esaltazione di un contrasto simultaneo?
Direi che certamente questo è vero, anche se l’esperto in materia è ovviamente Davide Barranca. Il perché gli aloni funzionano fino a un certo punto è legato al fatto che gli stessi si fondono con l’immagine a causa della risoluzione del nostro occhio: se avessimo una risoluzione più elevata risulterebbero dolorosamente visibili. Ma certamente il contrasto simultaneo (che riguarda anche la sola L, non solo il colore) entra in gioco. La tecnica di utilizzare la maschera di contrasto sui canali a e b ideata da Margulis va esattamente in questa direzione, e se è vero che certe volte non funziona bene è anche vero che quando funziona è assolutamente spettacolare. Molto image-dependent, naturalmente. A presto e grazie, Eugenio!
I vantaggi dell’essere laureato in ing. arospaziale non sono tanti in fotografia. Poter leggere in 5 minuti questo articolo e capire perfettamente i tuoi processi mentali e logici è uno di quelli.
Ho provato anche io, spesso, a spiegare concetti con analogie fisiche o addirittura sociali, politiche anche (credo fermamente nella frase “il principio é più importante del dettaglio”. Frase del fluidodinamico Von Karman che è la sintesi del mio modo di agire e vivere le analogie della vita) ma non ho mai raggiunto il tuo tipo di struttura e linearità (che ti caratterizzano). Il fatto è che “il principio é più importante del dettaglio” mi impone sempre descrizioni più vaghe e sospese ed è questo il motivo per cui non potrei mai insegnare un tubo a nessuno ma solo imparare da persone come te.
Giuseppe
Giuseppe, non credo di meritare tanto. Il principio che uso è molto semplice: cerco analogie che si possano comprendere con un po’ di sforzo, e cerco di nascondere lo sforzo. Il mio modello è Richard Feynman: i suoi diagrammi li può capire intuitivamente un bambino delle elementari, ma nascondono una complessità spaventosa che si manifesta quando i sistemi che si studiano diventano complessi. Molto tempo fa, probabilmente in un suo libro, lessi quello che era il suo principio didattico. A memoria, diceva qualcosa del genere: quando penso a un sistema parto da una sfera. Sistema a due corpi? Ah, no, due sfere. Facciamole una rossa e una verde. Con attrito? Ok, sfere pelose. E da lì diramava braccia, connessioni, cercando di modellare qualcosa di comprensibile. Credo che sia uno dei più grandi metodi didattici che io abbia incontrato, anche se non mi ritengo di certo uno specialista nel campo della didattica. In realtà è più complicato di quanto sembri: quando si inizia a ragionare troppo spesso per modelli si corrono due rischi; il primo è quello di generalizzare e perdere di vista le sfumature (sono d’accordo sul rapporto principio-dettaglio, ma ci sono casi in cui anche il dettaglio conta molto); il secondo è quello di non venire compresi, perché si cerca di calare la realtà in un mondo di sfere pelose, colorate e piene di braccia che a volte non stanno simpatiche. Alcune persone hanno bisogno di mondi più quadrati, più lineari, in cui “questo va qui e quello va lì”. E allora possono essere dolori.
Grazie mille, in ogni caso!
Eugenio,
gli artefatti della maschera di contrasto sono percepiti come “naturali” (entro certi limiti) perché riproducono il fenomeno delle bande di Mach (vedi qui, se lo sfondo del sito che sto per linkare non ti accieca http://www.nku.edu/~issues/illusions/MachBands.htm). Sostanzialmente i fotorecettori della fovea sono disposti in una geometria a mezza strada tra il nido d’ape e la ciambella (semplifico): ovvero raggruppati in insiemi circolari di due tipi, nei quali il centro reagisce diversamente dalla periferia. In un caso, il centro è collegato a terminazioni nervose la cui risposta viene stimolata dal bombardamento di fotoni mentre la risposta periferica ne è inibita; nell’altro caso è vero il contrario. Per fartela breve, questa disposizione è la ragione per cui, quando guardiamo una scala di questo tipo (http://www.nku.edu/~issues/illusions/Images/Mach/MachBands.jpg) percepiamo (delle bande di Mach) una sorta di naturali gradienti tra una zona tonale e l’altra. Che sono parenti stretti della maschera di contrasto.
Grazie mille, DB! 🙂
Articolo stimolante. Molto stimolante. È ammirevole la tua capacità di scrittura. Il modello del dipolo magnetico è affascinante. Ma se ora mi si ponesse la domanda su quantii sono i primari in Lab, prenderei tempo. Faccio molta fatica a considerarli solo 2. Provo a spiegarmi: siamo partiti da Hering il quale sosteneva che un oggetto rosso (magenta per noi) non possa essere al contempo verde; e che un oggetto giallo non possa essere al contempo blu. E siamo arrivati alla conclusione che un oggetto magenta è in realta semplicemente meno verde; e un oggetto giallo è semplicemente meno blu. Probabilmente è un concetto che richiede maggior riflessione. Anche perché finora io semplificavo in questo modo: noi percepiamo, per mezzo dei tre tipi di cono, le lunghezze d’onda lunghe (R), medie (G) e corte (B). Il che per me spiega sia la sintesi additiva RGB sia quella sottrattiva CMY. La prima in modo additivo, la seconda in modo sottrattivo, determinano la composizione delle lunghezze d’onda che vanno a colpire la nostra retina e che costituiscono i segnali in entrata. Per il metodo Lab, l’analogia io la vedevo con il modo che ha il nostro sistema visivo di organizzare i segnali in uscita dalla retina verso il cervello. E cioè attraverso tre canali separati che codifiano le differenze tra bianco e nero, magenta e verde e giallo e blu. I canali a e b mi appaiono allora non come dei primari ma come il risultato di una elaborazione che mi sta ad indicare le rispettive quantità di R di G e di B.
Ancora una volta, grazie. Ciao
Grazie Luca. Quello che scrivi è tutto corretto, ma continuo a ritenere che sia più lineare (al di là dell’apparente difficoltà concettuale) pensare ai colori primari di Lab come dei dipoli uniti e indivisibili: di fatto, un unione di due tinte in un tutto unico. Sto lavorando a una certa idea da un po’ di tempo e appena l’avrò messa a fuoco penso di scriverne, ma il succo è il seguente.
A monte di tutta questa faccenda c’è un principio fondamentale dell’algebra lineare, che è quello di indipendenza lineare. Questo c’entra con ciò che facciamo, perché in ultima analisi gli spazi colore non sono altro che spazi vettoriali. In parole povere, noi possiamo definire uno spazio tramite quella che viene denominata base dello spazio stesso. Una base si costruisce di norma con elementi che siano linearmente indipendenti tra loro, ovvero si richiede che nessun elemento sia ricavabile da combinazioni degli altri. Se cade questo principio, ci sono diversi problemi che entrano in scena. In RGB, i tre primari sono linearmente indipendenti perché nessuna combinazione di R e G (ad esempio) può produrre B, e questo vale per tutte le permutazioni dei primari. In CMYK è diverso: i primari sarebbero C, M e Y, e K è stato buttato nel mucchio per le note problematiche legate alla stampa. Se ipoteticamente avessimo degli inchiostri di luminosità e saturazione pari ai secondari di RGB costruiti come combinazioni (intendo 100Y = 255R + 255G, e via dicendo), CMY sarebbe di fatto identico a RGB: il canale C sarebbe uguale al canale R, M a G, e via dicendo. Non avremmo a priori bisogno di K (anche se – buona fortuna a stampare un testo nero a registro, nella pratica). Ma le cose non vanno così, e ci serve il nero. La grande differenza di CMYK rispetto a RGB consiste nel fatto che K è di fatto esprimibile come combinazioni di C, M e Y, e quindi i quattro elementi CMYK non formano una base linearmente indipendente. Per fare un esempio praticao, un colore come 19K è equivalente a 18C13M14Y (all’interno del profilo standard Coated FOGRA39), e questo genera tutta la storia dei profili CMYK a GCR diverso e ci regala il famoso potere del nero, che permette di lavorare sulle ombre in maniera più efficace che in qualsiasi altro metodo colore.
L’indipendenza lineare, però, è richiesta solo all’interno di un dato spazio: nel momento in cui passo da RGB a Lab posso benissimo definire L, a e b in termini legati a RGB, anche perché altrimenti mi mancherebbero i mezzi per poter convertire da uno spazio all’altro. Quindi il tuo punto di vista è corretto: a e b sono di fatto pensabili come combinazioni di R, G e B (anche se non è così ovvio costruire le formule), ma sono anche dei primari in senso stretto perché sono linearmente indipendenti tra loro. Ovvero, i due punti di vista non sono in contraddizione, a mio modo di vedere.
Sono argomenti complicati e pieni di insidie, e non è così facile venirne fuori, ma sono anche molto stimolanti a mio modo di vedere. Quello che ho in mente è la possibilità di estrarre delle informazioni di saturazione dai canali RGB con un metodo che Tonalità/saturazione non può mettere in atto perché la definizione della saturazione in HSB (e metodi simili) è tutt’altro che corrispondente a ciò che percepiamo. Quindi, vediamo se nel tempo riuscirò a scrivere qualcosa di sensato sull’argomento :-).
Grazie dei tuoi commenti sempre stimolanti!
Grazie a te Marco. Sei un punto di riferimento.
Per quanto riguarda il pensare ai colori primari in Lab come a dipoli indivisibili, temo che il mio problema non sia solo capirlo ma soprattutto “vederlo”. Se penso in termini di RGB, riesco a vedere tali componenti in qualsiasi colore: un Giallo può avere un po’ di rosso in più, come nel giallo arancio; o avere più verde come in un giallo limone. In maniera analoga, anche nel Magenta e nel Ciano è facile “vedere” quale componente domina. In Lab, (adesso la dico grossa tanto posso dare la colpa all’orario), penso ai valori negativi come in sintesi addtiva (a) sta per G e (b) sta per B, la cui combinazione mi produce qualche variante di Ciano; e penso ai valori positivi come in sintesi sottrattiva: a sta per M e b sta Y così che sottraendo dal Bianco (RGB) rispettivamente il verde e il blu, insieme mi producono qualche tipo di rosso.
Il tuo modello è per me un punto di vista nuovo. Ma è anche per questo che leggo tutto i tuoi articoli.
Grazie ancora.
Questo è un modo di pensare che funziona e rende in qualche modo le cose più semplici. Io spesso ho detto cose come questa: “il rosso si costruisce col giallo e col magenta, quindi a > 0 e b > 0, il cyan con il verde e col blu, quindi a < 0 e b < 0." Così facendo e limitandomi a questo, però, mischio selvaggiamente sintesi additiva e sottrattiva come se niente fosse e senza spiegare perché: si tratta solo di una regola mnemonica. A tutti gli effetti, perlomeno dal punto di vista fenomenologico, i conti tornano - e questa "stenografia" è solo un modo diverso di dire quello che tu hai appena affermato. Il problema, semmai, è nella tua frase "...in RGB, riesco a vedere tali componenti in qualsiasi colore" - se la interpreto correttamente. "Qualsiasi" non è vero: puoi far virare un giallo verso il rosso o verso il verde - ma non verso il blu. Il blu è e rimane un colore opponente del giallo, indipendentemente da come formuliamo il modello, e se possiamo idealmente spingere un pompelmo con continuità a diventare un'arancia (verso R) o un cedro (verso G), non possiamo spingerlo a diventare blu (sempre con continuità) a meno che non lo neutralizziamo completamente a un certo punto. In altri termini, il passaggio giallo -> arancione, con l’aggiunta del rosso, è pensabile in maniera continua, mentre il passaggio giallo -> blu attraversa necessariamente una fase in cui il giallo “scompare” per diventare blu. Per scomparire deve neutralizzarsi, ovvero diventare “grigio”. A meno che, naturalmente, non facciamo virare tutto il colore come avviene con il cursore Tonalità in Tonalità/saturazione, ma quella è un’altra storia.
La non-possibilità di coesistere, per due colori opponenti, è alla base dell’idea di Hering. Il riferimento all’esperimento di Crane e Piantanida del 1983 citato nell’articolo segnala che questa idea è ancora in discussione e non è chiara, così come non è chiaro come avvenga la ricombinazione dei segnali RGB nel momento in cui percorrono il nervo ottico per arrivare al cervello. L’esperimento venne poi ripreso da altri ricercatori, ma che io sappia non ci sono risultati definitivi e assodati a disposizione. Questo io lo chiamo “vivere in un mondo interessante” :-).
Marco, hai perfettamente ragione. Non posso vedere del blu nel giallo. E quando ho scritto “riesco a vedere tali componenti in qualsiasi colore” non intendevo dire che riesco a immaginare qualsiasi colore; intendevo dire che qualsiasi colore “reale” riesco a vederlo in termini di RGB. Comunque stanotte il mio cervello deve aver rielaborato molte cose e mi è venuta un’idea che al momento mi pare buona. Provo a fare qualche verifica empirica e poi te la scrivo, mi piacerebbe un tuo parere. Grazie
Marco, provo a descriverti il mio ragionamento.
Nella retina, i tipi di coni sono tre e quindi, per quanto riguarda l’aspetto cromatico, il segnale luminoso viene scomposto nelle componenti RGB. In modo analogo funziona il sensore della fotocamera.
Ora, per come la vedo io, il problema è quello di trasferire le informazioni cromatiche RGB utilizzando 2 canali al posto di tre.
Per risolvere il problema prendo in prestito il tuo modello della bilancia, con qualche variazione. La bilancia che propongo ha un braccio più lungo dell’altro, ed è quello che sorregge il piatto destinato alla misura dei pesi negativi. L’equilibrio si ottiene quando ad una quantità posta sul piatto negativo corrispondono due quantità sul piatto positivo.
Il piatto negativo può pesare solo G oppure B; quello positivo solo R e B (Magenta) oppure R e G (Giallo).
I piatti positivi possono ospitare solo parti uguali di R e B o parti uguali di R e G.
Quando R è accompagnato a B il valore misurato verrà registrato nel canale a; se è accompagnato a G, nel canale b.
I valori misurati per G verranno registrati nel canale a; quelli di B nel canale b.
In condizioni di equilibrio, quindi, i valori R, G e B corrispondono e si ha la neutralità. Ma negli altri casi, come dovrebbe funzionare la conversione?
Provo a spiegarlo partendo da un caso concreto R93; G103; B69.
Per prima cosa viene individuato il valore più basso e lo si sottrae a tutti e tre i valori misurati; in questo modo si elimina la componente grigia e si elimina anche un canale; rimaniamo quindi con R 24 e G 34;
Seconda operazione: rimangono R e G; ma poiché devono essere presenti in parti uguali, mantengo R24 e G24; 24 sarà quindi il valore di b;
Rimango quindi con un eccesso di 10 unità di G. E (10) sarà il valore negativo di a.
Concretamente R93; G103; B69 corrispondono in Lab a L42 a(9) b18. I valori che ho invece trovato io sono a(10)b24, per cui immagino che nella conversione reale entrino in gioco altri fattori.
Quello che m’interessa è capire se il modello è funzionante o se pecca di qualche errore grossolano.
Personalmente riesco a pensarlo anche a livello retinico.
Spero di essere stato abbastanza chiaro.
Grazie per averlo letto, ciao.
La linea di pensiero è interessante, e la rimozione della componente grigia è quello che di fatto si fa per stabilire che colore corrisponde a una terna di valori RGB. Io ci sto pensando da un po’ ma lungo una linea un po’ diversa, che curiosamente però porta comunque a far pesare la componente magenta (R+B) e la componente gialla (R+G) metà dell’altra. Questo esce da considerazioni puramente algebriche, tra l’altro, quando si impone che la neutralità in RGB si traduca in a = 0 e b = 0.
Tieni comunque presente che questo è un modello accademico: non esiste, che io sappia, una formula di conversione diretta da RGB a Lab anche perché RGB significa poco se non specifichiamo il profilo. Mi risulta che il metodo canonico sia passare per uno spazio intermedio, XYZ, che si correla poi direttamente a Lab da un lato e a RGB dall’altro.
Ma… se hai pazienza qualche giorno ne scriverò nel prossimo articolo, che è stato stimolato proprio dalla tua osservazione di ieri sull’espressione di a e b tramite combinazioni di R, G e B. a e b “veri”, di per sé non funzionano come ci si aspetterebbe, ma dei canali fittizi molto simili ad a e b si possono costruire, questo sì. E possono avere un’utilità notevole in certi contesti, pur senza uscire mai da RGB. OK, suspence… 🙂
OK, un errore del modello l’ho già trovato da solo. Ad esempio se i valori di partenza sono R100; G0; B0. Quindi, R e B oppure R e G non devono essere necessariamente uguali. Forse bisogna mantenere il valore di R in ogni caso ed distribuirlo nei due canali. Mah, ci penserò meglio.
Scusa, ciao
Piccola curiosità da ignorante. Il fenomeno descritto delle bande di Mach può essere in qualche modo ricondotto all'”effetto Moirè” o si tratta di un altro fenomeno? Se fosse così, la riduzione di tale effetto si potrebbe affrontare utilizzando in qualche modo il principio di isolare le frequenze spaziali come per la maschera di contrasto? (anche se funzionano benissimo molto spesso le maschere ottenute dalla manipolazione dei canali a e b di Lab…a proposito dell’articolo). Grazie.
Innanzitutto, da dove nasce il moiré: è un effetto ottico che deriva dalla sovrapposizione di due pattern regolari. L’interferenza tra i due ne forma un terzo, che è quello che percepiamo come moiré. La parola chiave è “pattern”, ovvero schema regolare e ripetitivo. All’epoca della pellicola il problema non esisteva, perché i granuli che formavano l’immagine erano disposti in maniera casuale, a differenza di quanto avviene con gli elementi del sensore che sono rigidamente disposti in forma di array.
Questo implica che il moiré è un effetto reale, ovvero la variazione indesiderata di colore e luminosità è presente nell’immagine. Le bande di Mach invece dipendono da come funziona il nostro occhio, come ha spiegato Davide, e derivano dalla differenza di reazione dei fotorecettori nell’occhio a seconda delle terminazioni nervose coinvolte. È quindi, se vogliamo chiamarla così, un’illusione ottica e non una caratteristica dell’immagine. Dipende dalla nostra ricezione del segnale, e non dal segnale – a differenza del moiré.
Quindi sono due fenomeni ben distinti, direi, e non collegabili a quanto riesco a vedere. Non escludo, naturalmente, che ai bordi delle frange del moiré possa verificarsi un fenomeno percettivo analogo a quello delle bande di Mach, ma questo è un fatto aggiuntivo – semmai.
Ciao Marco, innanzitutto complimenti, dato che affronti il tema “colore” con un equilibrio perfetto tra scientificità e tenore divulgativo (a volte un po’ prolisso, ma va bene cosi).
La mia domanda è sul tuo inciso: “I valori HSB, per inciso, dipendono dalle impostazioni di RGB.”
Ho trovato su [http://www.rapidtables.com/convert/color/rgb-to-hsl.htm] le formule di conversione da RGB a HSL, che ho implementato in Excel (non banalissima implementazione), e sembrano funzionare alquanto.
La domanda è: dove s’inserisce lo Spazio Colore di RGB in queste formule? nelle stesse, pubblicate sul sito, lo s.c. non interviene come una variabile del computo.
Grazie, Maurizio.
Maurizio,
grazie innanzitutto dei commenti, mi fa piacere che trovi utili gli articoli.
La prima osservazione è che HSL è simile ad HSB ma non coincidente con esso. I modelli sono quattro: HSL, HSB/HSV (stessa cosa), HSI. H sta per Hue, S per Saturation e le altre lettere corrispondono rispettivamente a Lightness, Brightness/Value, Intensity. La differenza non è essenziale in questo contesto.
In ogni caso, in HSB un colore come 255R 0G 0B corrisponde a 0H 100%S 100%B. Naturalmente il colore percepito dipende dalle caratteristiche dello spazio colore RGB: cromaticità, gamma, etc.
Il risultato netto è che 0H 100%S 100%B corrisponderà comunque al massimo rosso che si può realizzare in un dato RGB, e il colore percepito cambierà comunque in relazione alle caratteristiche dello spazio RGB nel quale operiamo. In parole povere, 0H 100%S 100%B rappresenterà un rosso diverso a seconda che lo riferiamo a sRGB o a ProPhoto RGB, per fare un esempio.
Questo accade perché la trasformazione che porta da RGB all’equivalente HSB è in pratica una semplice trasformazione geometrica: tolti pochi casi specifici, per ogni terna RGB esiste una terna HSB e viceversa. A differenza di quanto avviene, per esempio, mettendo in corrispondenza RGB com CMYK, non possono esserci né colori duplicati né colori fuori gamut, anche se esiste il caso degenere di S = 0% in cui si ottiene un grigio che dipende solo da B (più o meno chiaro, quindi) indipendentemente dal valore di H. Anche il caso di B = 0% è particolare: se la brillanza è zero, qualsiasi tinta a qualsiasi saturazione si manifesta come un colore nero. Quindi un colore come 0H 100%S 0%B è identico a 60H 70%S 0%B e coincide con 0R 0G 0B per qualsiasi coppia di H ed S. Tolti questi casi ridondanti, tutto funziona a dovere.
Onorato di una tua risposta!
Allora, se capisco bene, non ha senso parlare di HSL/HSB, ma si dovrebbe parlare di HSL/HSB() (invece, non lo si fa, ci si riferisce genericamente a un’equivalenza con R,G,B (0..255)).
Si dà forse per scontato che l’HSL/HSB si riferisce per default ad uno sRGB?
Inoltre, ad esempio, mentre il colore HSL H120°,S0%, B50%(sRGB)=(0,255,0) (Verde saturo in sRGB), l’ HSL H120°,S0%, B50%(ProPhotoRGB) dovrebbe coincidere col Verde puro di ProPhotoRGB e dunque ricadere al di fuori del range di visibilità…
Errata Corrige: nel post è sfuggito del testo, l’avevo messo tra tag:
“Allora, se capisco bene, non ha senso parlare di HSL/HSB, ma si dovrebbe parlare di HSL/HSB(-spazio RGB di riferimento-)”…
Allora – un buon articolo sulle differenze tra i vari spazi “HS-qualcosa” è reperibile su Wikipedia. In sostanza le differenze tra le definizioni dei vari spazi HS* sono essenzialmente matematiche: tutti rappresentano RGB solo che utilizzano altre coordinate per farlo. Un matematico direbbe che la trasformazione da RGB a HS* è una trasformazione da coordinate cartesiane a coordinate cilindriche. L’articolo osserva giustamente che le definizioni non sono del tutto standardizzate, anche se c’è una discreta consistenza.
In ogni caso, considerando un RGB generico si può costruire, ad esempio, il suo equivalente HSB. Il rosso più intenso che rappresenti in HSB sarà corrispondente a 255R 0G 0B. Quale rosso sia effettivamente dipende dall’RGB di cui parliamo. Pertanto uno spazio HSB coprirà il gamut di sRGB, Adobe RGB, ProPhoto RGB o qualsiasi altro RGB abbiamo in mente nel momento in cui specifichiamo a quale RGB stiamo pensando. Il fatto che poi un certo colore possa cadere fuori dal range di visibilità non è un problema, perlomeno non lo è più di quanto già non sia in RGB. Se una certa formula HSB ci fornisce un colore non rappresentabile, il suo equivalente RGB sarà a sua volta non rappresentabile, e verrà approssimato opportunamente su un dispositivo di output in base a un determinato intento di rendering.
Le rappresentazioni si scelgono spesso per ragioni di semplicità: descrivere, ad esempio, la forma di una spirale di Archimede è un incubo in coordinate cartesiane (x, y) ma di una semplicità assoluta in coordinate polari (r, theta). La curva però non cambia: viene solo descritta più o meno semplicemente. Altre curve si descrivono invece più facilmente in coordinate cartesiane (o in altri sistemi ancora). Lo stesso discorso vale per i colori espressi in uno spazio colore piuttosto che in un altro.
Ciao Marco,
è la prima volta che ti scrivo e innanzitutto ti faccio i complimenti e ti ringrazio sentitamente per questa interessantissima risorsa che ci metti a disposizione… non è facile trovare sul web (o in generale) spazi dedicati a questi argomenti che possano vantare un approccio tanto interessante e approfondito!
Ho letto con molto interesse il tuo articolo, utilissimo per chiarire alcuni dubbi che avevo, ma avrei bisogno di un ulteriore delucidazione e cioè il perché le coordinate L, a e b siano assolute… il fatto che RGB dipenda dallo spazio colore utilizzato mi appare chiaro, ma mi verrebbe da pensare che anche per Lab valga lo stesso, cioè che tra i due fondamentalmente si operi solo un cambiamento di sistema di riferimento, e invece a quanto pare no!
Ti ringrazio in anticipo per il tempo che mi potrai dedicare, se non hai modo di dilungarti e sapessi comunque indicarmi una qualche risorsa alla quale attingere per chiarire i miei dubbi te ne sarei grato!
A presto e ancora complimenti!
Luca, innanzitutto grazie dell’apprezzamento.
È come dici, ma bisogna fare una precisazione. Il termine “Lab” ha in realtà diversi significati, ed esiste più di uno spazio colore “Lab”. In Photoshop però ce n’è uno solo, e per questo non si menzionano varianti. La variante di Photoshop è quella denominata CIELAB 1976.
C’è un articolo di Adobe (abbastanza stringato, a dire il vero) a questo link: http://web.archive.org/web/20081207061220/http://kb.adobe.com/selfservice/viewContent.do?externalId=310838
A presto!
MO