Oggi è il 6 gennaio, festa della Befana. Vorrei pertanto iniziare questo articolo con una rima di grande spessore letterario:
La Befana vien di notte
con le scarpe tutte rotte:
vi regala una teiera
che però, forse, è chimera.
Prima di dichiarare la mia infermità mentale, vi invito a leggere almeno un po’ avanti.
Un solo uomo, milioni di idee
 Chi ricorda Bertrand Russell? È da sempre uno dei miei eroi perché non aveva paura del dubbio. Filosofo, logico, autore dei Principia Mathematica assieme ad Alfred North Whitehead, premio Nobel per la letteratura nel 1950, a 78 anni: “quale riconoscimento ai suoi vari e significativi scritti nei quali egli si leva in alto a campione degli ideali umanitari e della libertà di pensiero”. La sua ben nota antinomia nota come Paradosso di Russell mise in crisi i fondamenti della matematica ed ebbe ripercussioni forse non ancora comprese fino in fondo (basti pensare alle implicazioni dei due teoremi di incompletezza formulati da Kurt Gödel proprio per risolvere il problema). Morì nel 1970, alla soglia dei 100 anni di vita, e quindi non fece in tempo a conoscere Photoshop. Credo però che se oggi fosse vivo avrebbe qualcosa da dire su alcuni preconcetti che attraversano il nostro campo di azione e metterebbe in riga diverse idee sbagliate che ci trasciniamo dietro da tempo.
Chi ricorda Bertrand Russell? È da sempre uno dei miei eroi perché non aveva paura del dubbio. Filosofo, logico, autore dei Principia Mathematica assieme ad Alfred North Whitehead, premio Nobel per la letteratura nel 1950, a 78 anni: “quale riconoscimento ai suoi vari e significativi scritti nei quali egli si leva in alto a campione degli ideali umanitari e della libertà di pensiero”. La sua ben nota antinomia nota come Paradosso di Russell mise in crisi i fondamenti della matematica ed ebbe ripercussioni forse non ancora comprese fino in fondo (basti pensare alle implicazioni dei due teoremi di incompletezza formulati da Kurt Gödel proprio per risolvere il problema). Morì nel 1970, alla soglia dei 100 anni di vita, e quindi non fece in tempo a conoscere Photoshop. Credo però che se oggi fosse vivo avrebbe qualcosa da dire su alcuni preconcetti che attraversano il nostro campo di azione e metterebbe in riga diverse idee sbagliate che ci trasciniamo dietro da tempo.
Non un post, ma una serie
Questo post è il numero 0 di una serie intitolata “La teiera di Russell e Photoshop”, in omaggio a un famoso articolo commissionato all’autore nel 1952. La storia della teiera è un vero e proprio manifesto della libertà di pensiero e vorrei riassumerla brevemente.
Russell afferma che l’ipotesi dell’esistenza di una teiera di porcellana situata tra la Terra e Marte e in rivoluzione attorno al sole è impossibile da contraddire: a patto di aggiungere che la teiera è troppo piccola per essere visibile, con qualsiasi telescopio. Non fa una grinza: non si può smentire a priori l’esistenza di qualcosa che non è osservabile. Russell però mette in guardia da un passo successivo, fin troppo facile da prevedere:
Ma se io dicessi che, giacché la mia asserzione non può essere smentita, dubitarne sarebbe un’intollerabile presunzione da parte della ragione umana, si penserebbe giustamente che stia dicendo fesserie. Se però l’esistenza di una tale teiera venisse affermata in libri antichi, insegnata ogni domenica come la sacra verità e instillata nelle menti dei bambini a scuola, l’esitazione nel credere alla sua esistenza diverrebbe un segno di eccentricità.
Una botta in testa a ogni integralismo, dunque: di qualsiasi segno.
Un postulato fondamentale
Perché mi piace tanto questa teiera? Il motivo è che in questa serie di articoli vorrei discutere su basi realistiche alcuni pregiudizi che caratterizzano diversi argomenti di nostro interesse. Annuncerò gli argomenti mano a mano che gli articoli appariranno, e in questo post preliminare ho intenzione di introdurre alcuni concetti ai quali mi riferirò in seguito. Dovrete avere un po’ di pazienza, almeno stavolta, perché devo allestire un piccolo terreno di gioco adatto a ospitare gli argomenti dei quali parleremo. Innanzitutto, visto che da qualche punto bisogna partire, vorrei partire da un postulato fondamentale: un’ipotesi di lavoro, se vogliamo. Come tutti i postulati, questo si può naturalmente negare e chi legge è liberissimo di farlo; voglio solo che sia chiaro che mi riferirò a questo assunto costantemente. Il mio postulato è il seguente.
Due immagini indistinguibili a occhio nudo da parte di un osservatore umano medio possono essere considerate uguali indipendentemente da qualsiasi differenza riscontrabile con altri metodi di indagine.
Il postulato ha due implicazioni molto importanti.
- Se verifichiamo una qualsiasi differenza matematica nei valori numerici che definiscono le due immagini, ma tale differenza non produce alcun effetto visibile, dichiareremo quella differenza irrilevante.
- Una differenza rilevata da uno strumento che, di nuovo, risulti invisibile per un essere umano sarà parimenti irrilevante.

La logica di queste due implicazioni non è quella di denigrare l’elaborazione teorica o declassare le letture strumentali: anzi, si tratta di due aspetti estremamente importanti del nostro lavoro. Semmai, è quella di portare in primo piano una pratica operativa basata sul buonsenso: le operazioni che compiamo sulle nostre immagini o su quelle dei nostri clienti producono risultati che sono destinati alla fruizione da parte di nostri simili – genere Homo, specie Homo Sapiens Sapiens, discendenti diretti dall’Australopithecus Africanus. Questa discendenza è importante, perché implica che anche se siamo tutti diversi abbiamo in comune moltissime cose: tra queste, i meccanismi della percezione. Se crediamo al postulato esposto sopra, ben venga tutto ciò che può migliorare il nostro lavoro sulle immagini; ma prestiamo attenzione ai pregiudizi e ai preconcetti, spesso spacciati come vere e proprie verità di fede, che possono addirittura comprometterlo, o comunque impedirgli di raggiungere i massimi livelli qualitativi possibili.
Un esempio (veramente noioso)
Vorrei fare un esempio di ciò che intendo, e lo sceglierò così eclatante da risultare potenzialmente offensivo per l’intelligenza, solo per chiarire il concetto. Ho aperto un’immagine in Photoshop e impostato al massimo il fattore zoom di visualizzazione: 3200%. In questo modo i singoli pixel vengono visualizzati come quadratini di ragguardevoli dimensioni. Partendo dall’angolo in alto a sinistra, mi sposto di 500 pixel esatti in orizzontale e in verticale. Campionando il colore del pixel che ho individuato, per una volta con il contagocce impostato su Punto campione, scopro che le coordinate RGB nello spazio in cui l’immagine è codificata (ProPhoto RGB, a 8 bit) sono 119R129G166B. A questo punto, tramite il Selettore colore, imposto un nuovo colore: 121R131G168B, aumentando di due punti ciascuna componente RGB. Con lo Strumento matita, dimensione 1px, cambio colore al singolo pixel esaminato prima. Domanda: l’immagine che ottengo è diversa da quella precedente? Dal punto di vista strettamente matematico, sì: è differente in un punto e pertanto non può essere considerata identica. Dal punto di vista percettivo, no. Attenzione: se creiamo un documento, lo riempiamo uniformemente con il colore originale del pixel, 119R129G166B, e cambiamo colore a un singolo pixel utilizzando le nuove coordinate, su un buon monitor possiamo vedere la differenza. Ho provato: si vede! Ma questo avviene con un’immagine sintetica, anche se semplicissima. In una fotografia la possiamo vedere? Neppure in un milione di anni: perché i pixel che circondano quello da me originariamente prescelto variano tranquillamente di quantità pari e anche superiori alla variazione da me creata. Ovvero, c’è del rumore: molto contenuto, al limite dell’invisibile, ma pur sempre rumore: una fluttuazione casuale. D’altronde non vi sto mostrando l’immagine e potreste chiedervi quanto sia realmente rumorosa. Giusta domanda.
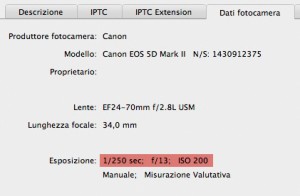
La prima risposta che posso dare sta nello screenshot dei dati contenuti nelle Info del file che ho aperto. Una fotocamera come questa, impostata su una sensibilità pari a ISO 200, con un’esposizione pari a 1/250 di secondo, non produce di norma un file estremamente rumoroso. Ma questa è, naturalmente, una considerazione basata sull’esperienza che non prova nulla. Proviamo in un altro modo: selezioniamo un’area significativamente ampia attorno al pixel scelto per la variazione, che si trova esattamente al centro della selezione quadrata visibile nell’immagine successiva, sulla quale potete cliccare per vederne una versione ingrandita. (Una nota: tutte le immagini in questo articolo sono state convertite in sRGB, pertanto se misurate i numeri non coincideranno con quelli che ho dato.)

Prima di mettere in atto una certa operazione che discuteremo tra poco, proviamo a individuare il pixel modificato. Probabilmente avrete capito che questo dettaglio enormemente ingrandito dell’immagine riguarda un cielo azzurro. Dove sta il pixel? Si trova al centro esatto della selezione, ma non contate le caselle: provate a vedere se a occhio vi appare un pixel significativamente diverso da tutti. Ovviamente, la risposta è no. Ora, la selezione misura 29 x 29 px, ovvero è composta da 841 pixel in totale. Filtro -> Sfocatura -> Media: tutta l’area selezionata viene riempita con un colore uniforme che è la media dei colori di tutti i pixel contenuti in essa: 120R130G167B, esattamente a metà tra i due colori citati prima – quello del pixel originale e quello da me scelto per la sostituzione.
A caccia di differenze

Se proviamo a esaminare pixel per pixel l’area mediata e quella originale, scopriamo naturalmente che i numeri dei colori sono diversi. Osservarlo è facile: basta sovrapporre a registro le due immagini (l’originale e quella con l’area mediata) in metodo di fusione Differenza e leggere i valori nel Pannello Info. Amplificando le differenze in maniera abnorme si ottiene il pattern casuale visibile nell’immagine a fianco. È casuale perché non presenta alcuna regolarità: stiamo solo osservando un rumore amplificato, e questo tipo di rumore è un fenomeno casuale. I diversi colori rivelano quali canali abbiano subito la massima variazione tra un’immagine e l’altra, ma il fatto essenziale è questo: i pixel neri corrispondono a nessuna variazione, quelli bianchi al massimo della variazione. All’esterno della selezione tutti i pixel sono neri perché non c’è alcuna differenza tra le due immagini: la media è stata calcolata solo all’interno dell’area quadrata. All’interno succede un po’ di tutto. Ma, di nuovo: siamo in grado ora che possiamo vedere chiaramente le differenze di individuare il pixel modificato in origine? No, a causa del carattere casuale del pattern. Se siete curiosi, senza farvi contare, vi indirizzo: il pixel in questione è color blu aviazione ed è circondato da quattro pixel con queste caratteristiche: a nord, magenta; a est, viola; a sud, giallo ocra scuro; a ovest, un pixel dello stesso identico color aviazione. Lo vedete ora? Con un po’ di fatica, lo avrete individuato. Ma la speranza di individuarlo a priori, anche osservando le differenze, è pari a zero.
A che serve tutto ciò?
Questa discussione non è affatto fine a se stessa. Ci siamo fissati su un singolo pixel per dimostrare che certe differenze sono totalmente irrilevanti nel contesto globale delle immagini. Non ho scelto ProPhoto RGB a caso: si tratta dello spazio colore con il gamut più ampio tra gli spazi RGB standard comunemente in uso. Lo ho scelto perché la sua estensione cromatica è enorme, ma ha lo stesso identico numero di colori di sRGB, Adobe RGB o qualsiasi altro spazio RGB: in 8 bit, 16.777.216 colori. Stesso numero di cubetti colorati, ma dimensione gigantesca: questo significa che quando passiamo da un cubetto all’altro la variazione è più ampia che in uno spazio colore con un gamut più ristretto. Se l’effetto non si vede in ProPhoto RGB, non si vedrà a maggior ragione in spazi colore più piccoli.
Se questo fosse poco chiaro possiamo osservare la seguente serie di campioni:

Sono partito da un colore pari a 150R30G20B in sRGB: lo vedete nel primo quadrato in alto a sinistra. I successivi nove quadrati sono stati riempiti con colori che progressivamente aumentano di due punti in ciascun canale: 152R32G22B, 154R34G24B e via dicendo. Successivamente, in un altro file, stavolta in ProPhoto RGB, ho calcolato l’equivalente del colore di partenza: 94R44G23B, e ho fatto la stessa operazione: i quadrati successivi sono stati riempiti con colori che aumentavano sempre di due punti in ciascun canale. Alla fine, conversione della sequenza da ProPhoto RGB a sRGB e affiancamento alla prima (sotto, nell’immagine riportata qui sopra). Il risultato è palese: la variazione in ProPhoto RGB, facendo passi della stessa lunghezza che in sRGB, è più ampia per il motivo che ho esposto.
Da un pixel a tutti i pixel
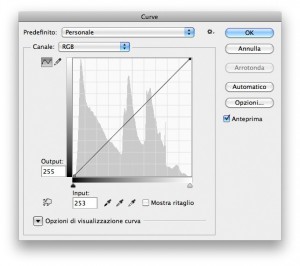
Il concetto che voglio chiarire con il mio esempio è semplice: in certi casi una differenza matematica esiste, ma non è percepibile. Quindi, in base al postulato, è come se non esistesse. Naturalmente sento l’obiezione in agguato: ho lavorato su un singolo pixel di un’immagine che ne misura 5442 x 3628, ovvero ne ha appena meno di venti milioni. “Per forza non si vedrebbe nell’immagine intera!” Quello che voglio fare ora è modificare tutti o perlomeno la grandissima maggioranza dei pixel di un’immagine. Lo farò con la curva di contrasto globale visibile in figura: il punto in basso a sinistra, relativo alle ombre, è spostato di due unità verso destra: Input = 2, Output = 0. Quello in alto a destra subisce un trattamento simmetrico: Input = 253, Output = 255. L’immagine originale è la prima qui sotto; la successiva è la stessa immagine sottoposta all’azione della curva. Prima della conversione per il web le due immagini erano in ProPhoto RGB.


La domanda è naturalmente se le due immagini appaiano diverse. Anche affiancandole alla massima risoluzione la mia risposta è: no. Altre cinque persone le hanno esaminate e la loro risposta è nuovamente: no. Non posso escludere che qualcuno dotato di eccezionale sensibilità al contrasto, alla luminosità e al colore potrebbe essere in grado di rilevare una minima differenza, ma ho serissimi dubbi in merito. Se desiderate provare, prestate attenzione al fatto che le disomogeneità locali di un monitor spesso fanno apparire diverse anche immagini affiancate rigorosamente identiche tra loro. Ovvero, se una vi dovesse sembrare più chiara, o più contrastata, o comunque diversa, provate a scambiarle, a osservarle sovrapposte in sequenza e via dicendo, in modo da essere certi di ciò che vedete.
Se trovassimo una persona su mille in grado di riscontrare ripetibilmente e con assoluta certezza una differenza, dovremmo accettare di trovarci ai margini del mio postulato, ma il peso statistico di questa eccezionale sensibilità sarebbe comunque molto basso: resterebbero novecentonovantanove persone su mille incapaci di decidere quale immagine sia quale. In aggiunta, se anche fosse possibile individuare un’area nella quale la differenza risultasse visibile esaminando l’immagine a fattori di ingrandimento enormi, questo sarebbe irrilevante, perché l’immagine ha senso nel momento in cui viene vista nel suo complesso; o anche ritagliata – ma la differenza rilevabile tra pochissimi pixel in un punto specifico, solo al microscopio, non sarebbe significativa. Quando guardiamo i pixel da vicino, non stiamo vedendo alcuna immagine, così come i singoli aghi di un pino non ci dicono nulla sulla foresta, intesa come entità a sé, in cui il pino si trova.

In realtà l’ultima eccezione sollevata è una preoccupazione debole in partenza perché, a causa di ciò che abbiamo discusso nella sezione relativa alla modifica di un singolo pixel nel cielo, quella differenza non potrebbe essere comunque visibile. Un pixel appena diverso dagli altri può essere visibile, a fatica, se è circondato da pixel rigorosamente identici: una disomogeneità risalta meglio all’interno di un’omogeneità perfetta. Ma nessuna area significativa di un’immagine fotografica è formata da pixel rigorosamente identici. Il cielo è la parte estesa più omogenea della nostra immagine, e qui sopra vediamo un’altra area ingrandita con un fattore di visualizzazione pari al 700%. Più di trentamila pixel sono in gioco e le variazioni sono di gran lunga più ampie che nel cielo: cambiando uno solo dei pixel, come prima, avremmo ancora meno chances di accorgercene, perché la microvariazione da noi indotta verrebbe soffocata da una variazione globale di gran lunga superiore a qualsiasi rumore realisticamente immaginabile. E, per di più, una variazione che descrive delle forme reali, non casuale.
Differenze ovunque, ma…
A questo punto, come prima, diamo un’occhiata alla differenza tra l’immagine originale e la versione curvata. La massima variazione riscontrabile nei singoli pixel è pari a 2R2G2B, esattamente la stessa variazione da me indotta a mano nel colore modificato per l’esperimento sul pixel del cielo. La mappa delle variazioni, enormemente amplificata, è questa:

Dove la mappa è neutra, la variazione riguarda la luminosità. Tutte le aree colorate indicano invece uno spostamento cromatico. Qui non abbiamo soltanto un pixel diverso: la schiacciante maggioranza dei pixel è stata modificata; in aggiunta, le variazioni non sono casuali, perché distinguiamo bordi e contorni degli oggetti. Tuttavia non percepiamo alcuna differenza tra l’originale e la versione curvata, quindi in base al postulato le due immagini possono essere dichiarate uguali per chi come noi discenda da una tribù di evoluti scimmioni. Il Pannello Info, naturalmente, non ha primati nel suo albero genealogico. Per questo motivo, ciò che il computer dice è irrilevante all’atto pratico: fino a che nessuno sarà in grado, con certezza e ripetibilmente, di scegliere la versione curvata nel momento in cui la vede affiancata all’originale, la discussione sulle differenze è fine a se stessa. Allo stesso modo, nel momento in cui la differenza fosse rilevabile con regolarità e ripetibilità, avremmo una sola possibilità: dichiarare che cadiamo fuori dal postulato; oppure che il postulato è sbagliato e va abbandonato. Così funziona la scienza, così dovrebbe funzionare il buonsenso.
JND, chi era costui?

Gustav Theodor Fechner, vissuto nel XIX secolo, fu uno dei padri della psicofisica. Anche se il peso delle sue idee si è ridimensionato nel tempo, alcune di esse rimangono di fondamentale importanza nello studio dei fenomeni legati alla percezione. In particolare, è fondamentale il concetto di Just-noticeable difference (JND), che possiamo tradurre con “differenza appena percepibile”. Il concetto è semplice: se veniamo sottoposti a uno stimolo che causa una percezione (stimolo di riferimento) e successivamente a uno stimolo che è una variazione del primo (stimolo secondario), il rapporto tra l’intensità della variazione e l’intensità dello stimolo di riferimento è con buona approssimazione costante. In parole molto povere, se la curva che applichiamo a un’immagine non causa una variazione sufficientemente significativa, siamo al di sotto della soglia JND e non percepiamo alcuna differenza. La codifica di questa legge è nota come legge di Weber-Fechner, e ha ricadute nella fisica, nella psicologia (la percettologia in particolare) e addirittura in campo economico.
Questa è la base sulla quale ci muoveremo in questa serie di articoli. Il postulato formulato all’inizio dell’articolo si basa sull’osservazione che esiste una JND descritta dalla legge appena citata. Russell avrebbe concluso probabilmente che, nel momento in cui la teiera non è osservabile perché troppo piccola, l’affermazione che essa non esiste ha lo stesso valore dell’affermazione opposta. Qui non si sta discutendo l’esistenza astratta di qualcosa, ma la rilevanza pratica della sua esistenza: perché le mappe di differenze mostrano che una variazione esiste, eccome; ma l’esperienza mostra che quella variazione non è percepibile, perché cade al di sotto della JND che caratterizza i sensi che utilizziamo per percepirla.
La meditazione finale è questa: se una teiera esiste ma non causa effetti percepibili sulla realtà, ha davvero senso perdere del tempo e preoccuparsene solo perché una macchina sostiene che esiste? E soprattutto, ha senso mettere all’indice chi osa sostenere che se la teiera non esistesse le cose sarebbero assolutamente uguali, nel nostro mondo?
Grazie per la pazienza con la quale avete seguito fin qui la mia lunga elucubrazione teorica. Nel prossimo articolo, prometto, ci sarà parecchio tè nella teiera, e avremo qualcosa di significativo su cui ragionare.
Buon tè pomeridiano a tutti!
MO



Caro Marco, assimilato il postulato aspetto con interesse
di leggere i prossimi sviluppi.
Un saluto
mi trovo in concordanza, perché, proprio oggi, in un post avevo scritto: se a una domanda che uno si fa, per esempio “perché questa disgrazia è capitata proprio a me?”, una religione non dà una risposta, in questo campo quella religione è inutile, anzi dannosa, perché ti fa credere che Dio ti ha mandato una disgrazia, ma tu non puoi saperne il motivo. Quindi la scienza è vero che non ti da delle risposte, però ti aiuta a far sì che tu non ti dia risposte sbagliate. A meno che Dio (se esiste) non ti abbia dato l’intelligenza perché tu debba rinunciare ad usarla.
Ugo, benvenuto sul blog e grazie di questo commento. Concordo in pieno: sono due livelli diversi che conducono a conclusioni diverse. A priori non critico nessuna scelta, ma in certi casi preferisco continuare a chiedermi “perché?” e a cercare una risposta. Per quanto ne sappiamo, siamo l’unica forma di vita sulla Terra in grado di porsi questa domanda, e se è così credo che un motivo ci debba essere.
Detto questo, il mio post non è sulla religione o contro di essa. È semmai contro la cecità del voler negare in maniera acritica certe evidenze, e questo per me vale in tutti i settori, ivi compreso Photoshop. È ovvio che in questo modo faccio una scelta di campo, ma perlomeno la dichiaro pubblicamente; e come ho scritto – ogni postulato si può rifiutare. E va benissimo così.
A presto!
L’osservazione di Ugo mi ha fatto venire in mente un episodio divertente e istruttivo. Quando ero studente di fisica all’università, un giorno passai assieme a un mio compagno di corso dalle parti della biblioteca e incontrammo una nostra compagna iscritta a matematica, decisamente esasperata.
«Cosa c’è?» le chiese il mio compagno.
«Non ne posso più! Sono due ore che cerco il professor X, sono stata in ogni ufficio possibile e sembra che dovunque io vada lui sia stato due minuti prima – ma non lo trovo!»
«È semplice,» disse lui, «fermati immobile nel punto dove sei ora e aspetta: il teorema di ricorrenza di Poincaré ti *garantisce* che entro un tempo di Poincaré il professor X passerà di qui. Tutte le configurazioni molecolari possibili si devono manifestare, quindi anche quella che lo porterà qui mentre ci sei tu.»
La compagna era confusa. Non studiando fisica non aveva ben chiaro il senso del teorema di ricorrenza.
«Ehm… quanto è lungo un tempo di Poincaré?»
«Circa 10 alla 23ma potenza», rispose il mio compagno. (Bastardo dentro, aggiungo io.) Seguì una memorabile domanda, e un’ancora più memorabile risposta.
«OK, dai, ho capito… ma… anni… secondi? 10^23 cosa?»
«Fa differenza?»
Ci allontanammo ridacchiando.
Molta, molta attenzione alle risposte sbagliate.
sono io uno dei mille… ? oppure è il mio monitor “uno dei mille”…?
Interessantissimo argomento, come sempre mi appassioni con le tue scritture, molto chiare anche per me…..
Ho ingrandito a schermo pieno l’immagine “08” ed anche l’immagine “09” su un’altra pagina, quindi cliccando prima su una e poi sull’altra posso confrontarle abbastanza bene (monitor 1280×1024), a prima vista sembrano identiche ma dato che mi hai incuriosito ho cercato la differenza …e l’ho trovata, l’immagine “09” è più scura, una differenza talmente pignola che solo uno come me, nota.
La differenza (sono un rompi….lo so) la si nota in particolare nell’ombra che proietta la scala di legno sull’edificio.
Dato che ho le immagini a schermo pieno, non credo che dipenda dal monitor, che come dici giustamente tu può variare a seconda della posizione dell’immagine, ed in effetti se confronto le due immagini come le hai postate nell’articolo, l’immagine “09” mi appare leggermente più chiara.
Sono uno dei mille che conferma il postulato….?
ciao e complimenti.
È vero: se mi concentro con la massima attenzione sull’ombra della scala una minima differenza si vede (a fatica), sul mio monitor. In misura ancora minore (a volte devo convincermi che la sto vedendo veramente, ti confesso) anche nei cespugli in basso a sinistra. Non a caso queste aree appaiono bianche, nella differenza, a significare che hanno la variazione massima in questa immagine. Non riesco a vedere la differenza se affianco le immagini, però, in nessuna combinazione possibile.
In generale non è del tutto corretto dire che l’immagine 09 (curvata) è più scura: lo è dai mezzitoni in giù, ma è più chiara dai mezzitoni in su – per effetto della curva.
In ogni caso, se una differenza è rilevabile, siamo ai margini estremi del postulato. Se faccio un blend al 50% della versione curvata con l’originale e la confronto con l’originale non riesco più in tutta onestà a essere sicuro che una differenza ci sia. La mia conclusione è, appunto, che siamo appena sopra la soglia della JND, con queste due immagini, perlomeno sul mio sistema attuale. Sul mio (fedele, ma infedele) monitor ausiliario, un CRT, non riesco a percepire assolutamente nulla, neppure con le due versioni originali.
Grazie della segnalazione – ma il succo del concetto a mio parere non cambia: esiste una soglia, dipendente da diversi fattori (comprese le condizioni di visualizzazione) sotto la quale le differenze sono di fatto trascurabili.
Semmai, comunque, sei uno dei mille che *mette in crisi* il postulato, non che lo conferma :-).
Avevo trovato stupendo il tuo articolo sul confronto tra 8 e 16 bit che credo di poter considerare come un’anticipazione di quanto ho letto ora.
Per la scelta dell’argomento e per come lo stai trattando ho soltanto un problema, non so più che aggettivi usare, ma penso che “meraviglioso” bossa andare bene.
Ora devo anche cercarmi qualcosa da leggere sia di Bertrand Russell sia di Gustav Theodor Fechner.
Come sempre, grazie.
Luca, grazie, ma non sopravvalutarmi. Sto solo seguendo una linea di pensiero che ho in mente da un po e non so bene dove porterà alla fine. In buona parte per me questo è imparare in pubblico, facendo anche degli errori, dei quali non mi vergogno affatto.
Hai comunque letto bene: la radice di questa serie sta proprio in quell’articolo del confronto tra 8 e 16 bit, su cui con calma vorrei tornare perché ho elaborato un po’ di cose in questi mesi.
Grazie ancora, a presto.
Resto sintonizzato con curiosità
Molto interessante! Attendo curiosa i prossimi sviluppi 🙂
anche secondo me la seconda immagine è più scura (ho un monitor Nec MultiSync P221w). Però misurando la differenza è veramente minima (su un pixel è 210,116, 62 contro i 208,116,64 della prima immagine). Vorrei invece aggiungere una variabile: la dimestichezza a valutare le immagini. Con il tempo mi sono accorto che ora percepisco meglio le dominanti o altre piccole differenze di colore, di quando ho iniziato a fare la correzione del colore. Secondo voi è possibile?
Credo proprio di sì, e certamente la famosa soglia della JND varia da persona a persona; e anche con le condizioni di osservazione influiscono, come abbiamo detto.
Quanto alla luminosità globale, è un problema difficile da discutere, a mio parere perché è largamente percettivo. Penso che molto possa dipendere dalla distribuzione delle zone di luminosità nell’immagine e al contrasto simultaneo che interviene tra esse. Un conto è se esaminiamo un singolo pixel (o un’area perfettamente omogenea estesa), un conto è se guardiamo un’immagine complessa. Nel caso che citi, i numeri rivelano che il pixel (210R 116G 62B) è più scuro di quello della prima immagine. La luminosità segue una formula che con buona approssimazione assegna questi pesi ai canali: 0,3 * R + 0,6 * G + 0,1 * B. Nel nostro caso, G è uguale e non causa variazioni di luminosità tra i due pixel; gli altri due canali sì: ma il peso dello schiarimento (30%) di R suggerirebbe una luminosità superiore per il pixel curvato, perché il peso dello scurimento (10%) dovuto a B è inferiore. Ovvero, globalmente dovremmo avere una luminosità maggiore. In realtà la differenza è così piccola che dubito davvero possa essere distinguibile: facendo finta di avere i decimali a disposizione siamo a 0,4 circa (su una scala da 0 a 255). In Photoshop il valore risulta essere 138 identicamente in entrambi i casi, ovvero non c’è differenza. Questo, naturalmente, a 8 bit. A 16 bit sì: una minima differenza rimane e le due luminosità risultano essere rispettivamente 17.766 e 17.718, con uno scarto di 48 punti che corrisponderebbe a 0,375 a 8 bit, in accordo con il calcolo derivante dalla formula citata sopra (ricordiamoci che la codifica di Photoshop non è a 16 bit, ma di fatto a “15+1”: i livelli sono 32.769, non 65.536 come ci aspetteremmo, quindi il calcolo si fa dividendo 48 per 128, non per 256). Grazie della tua osservazione!
Seduttore. Come altro potrei definirti?
Hai deciso di abbandonare le “pillole” e offrire calici di buon vino, seppur servito in teiere. Una grande bevuta, alla fine, in cui “sapersi ubriachi, volerlo essere ancora di più, è il primo passo verso una liberazione e il raggiungimento di quella ‘sobria ebrietas’ che porta alla lucidità e permette di intravedere il proprio cammino.”
Ho tanto da imparare. Imparo. Un calice alla volta… 😉
Bertrand Russell fece molto di più che causare una crisi nella matematica. Mise in crisi anche il metodo scientifico. Il ragionamento alla base della famosa teiera di Russell è assolutamente di tipo induttivo. Peccato però che lo stesso Russell sia la persona che l’inferenza induttiva nel metodo scientifico l’ha praticamente massacrata a partire dal famoso “tacchino induttivista”.
Kurt Godel con i suoi principi di incompletezza ci dice appunto che nessun sistema formale di regole che sia sufficientemente potente, autoreferenziale e ricorsivo può essere contemporaneamente completo e coerente.
Da un certo punto di vista si potrebbe dire che se un sistema formale di regole contiene tutte le verità, allora esiste almeno un paradosso. Se invece un sistema formale di regole non contiene paradossi e quindi è coerente, allora esiste almeno una verità che non può essere provata con il sistema formale di regole.
Nel raccontarci della sua teiera Russell introduce la parola “credere”. Si può infatti “credere” nella esistenza della teiera come si può “credere” (giacché come visto non tutte le verità sono dimostrabili…) alla sua “non esistenza” poiché per la ragione il problema è irrisolvibile. L’esistenza della teiera potrebbe essere una verità esterna al sistema formale di assiomi, principi e postulati dai quali discende tutto il sapere umano. Ma anche nel caso in cui si possa arrivare a un sistema formale più ampio che sia completo e che quindi contenga tutte le verità, l’esistenza della teiera potrebbe risultarci contemporaneamente sia vera che falsa e quindi il nostro sistema formale risulterebbe incoerente.
Da un punto di vista della logica formale non esistono “credenti” e “non credenti” ma sono entrambi credenti solo di cose opposte “credenti nell’esistenza” e “credenti nella non esistenza”. Chi si attenesse strettamente alla logica formale direbbe semplicemente che il problema è irrisolvibile.
Su tutto questo veglia sornione il gatto di Schrödinger. Amen. 🙂
Grazie mille, Roberto.