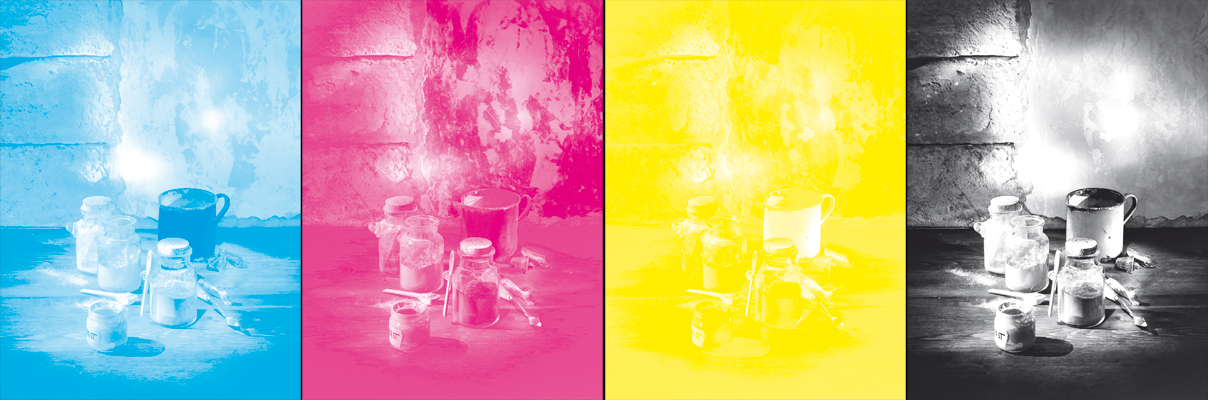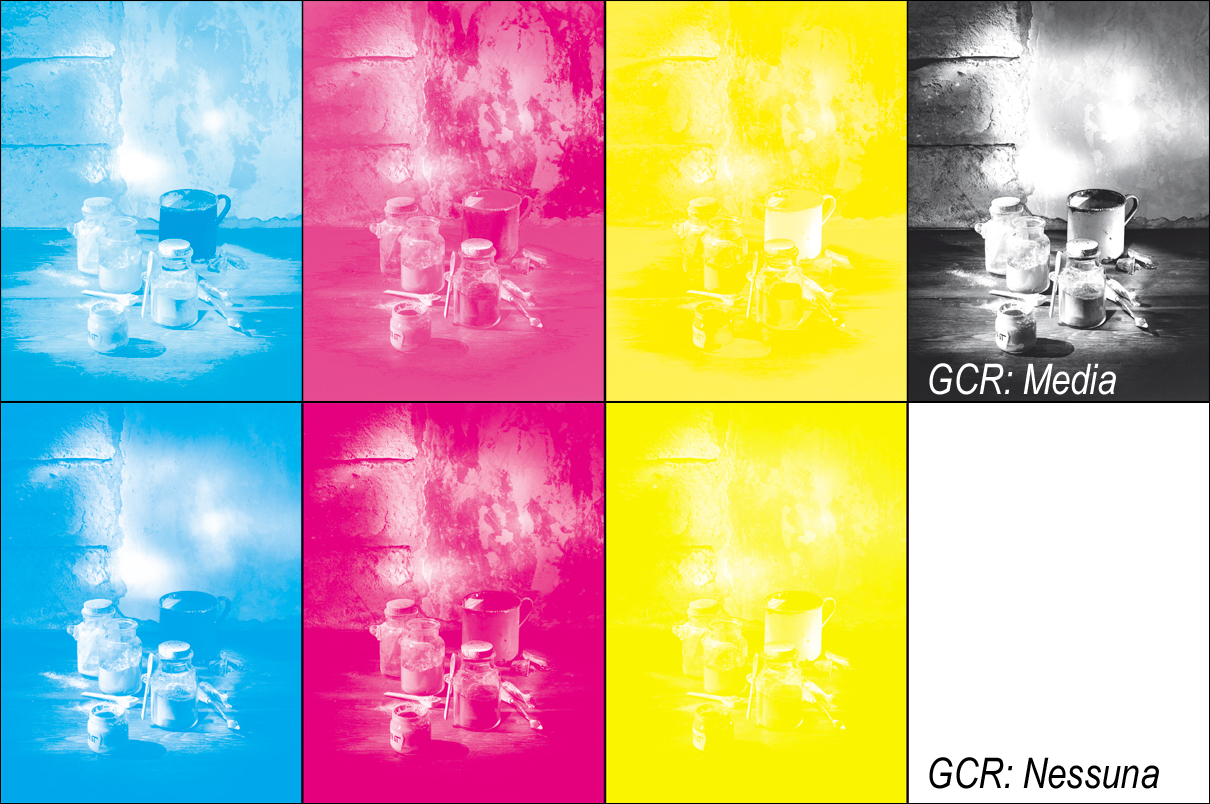Ringrazio ancora una volta Marco per l’ospitalità e per il coraggio, perché se state leggendo queste righe significa che l’ha pubblicato davvero. 🙂

Consideriamo una classe di 25 studenti: l’insegnante fa l’appello. Può farlo in positivo, contando i presenti, ad esempio 20,  e dedurre  il numero degli assenti: la classe al completo meno i presenti:

25 – 20 = 5.

Può farlo in negativo contando i banchi vuoti: mancano Fontana, Negri, Olivieri, Olivotto e Stefanini, e dedurre il numero dei presenti: la classe al completo meno gli assenti:

25 – 5 = 20.

Nel primo caso si arriva al risultato per mezzo di un’addizione, contando il numero dei banchi occupati. Nel secondo, in negativo, si contano i banchi vuoti, gli assenti, e lo si sottrae al numero che corrisponde alla classe al completo, 25.

Possiamo registrare il tutto su un foglio:

• in addizione, partiamo da un foglio vuoto e scriviamo il nome di ciascuno studente presente;
• in sottrazione, partiamo dall’elenco completo della classe e cancelliamo gli assenti.

Cambia il punto di partenza, ma il risultato è naturalmente identico.

In sostanza, che si ottengano le informazioni in positivo o che si ottengano in negativo,  il risultato non cambia.

Il concetto di negativo e quello di positivo è familiare a ogni fotografo, ma mi piace rivederlo alla luce dell’esempio fatto.

Consideriamo l’immagine astratta riportata sotto. Fotografiamola e proviamo a riprodurla. Per semplicità, immaginiamo di scattare con una Leica M Monochrom, senza filtro di Bayer e relativi problemi di interpolazione.

Ricordando Gulliver e spingendoci oltre, consideriamo ogni pixel della nostra fotocamera come una microscopica classe che, magicamente, al momento dello scatto si popola, in modo proporzionale alla luce che riceve, di microscopici studenti bianchi e luminosi, fino ad un massimo di 255 per pixel/classe.

(Caso vuole che tutti gli studenti abbiano lo stesso nome, Fotoni, e si assomiglino molto.)

Attenzione: da qui in avanti il modello non va preso alla lettera. Stiamo trascurando il fatto che i segnali raccolti da un sensore sono codificati a più di 8 bit e altre varie verità. Questo perché è importante il concetto, non il dettaglio.

Dunque, diciamo che ogni pixel può contenere da 0 a 255 Fotoni.

Dobbiamo ora usare le informazioni registrate nel sensore per riprodurre l’immagine in photoshop.

Non ci resta che fare l’appello contando i Fotoni, pixel per pixel. Abbiamo visto che possiamo farlo in due modi.

Partiamo dal più diretto, l’appello in positivo. In questo caso il livello di partenza è costituito da classi vuote e buie. Dobbiamo quindi contare i Fotoni presenti in ciascun pixel del sensore e aggiungerli ai pixel corrispondenti nel file creato con photoshop.

Sotto, il pannello Livelli con il livello di partenza.

Trasferiamo ora i nostri Fotoni dal sensore al livello vuoto del nostro file.

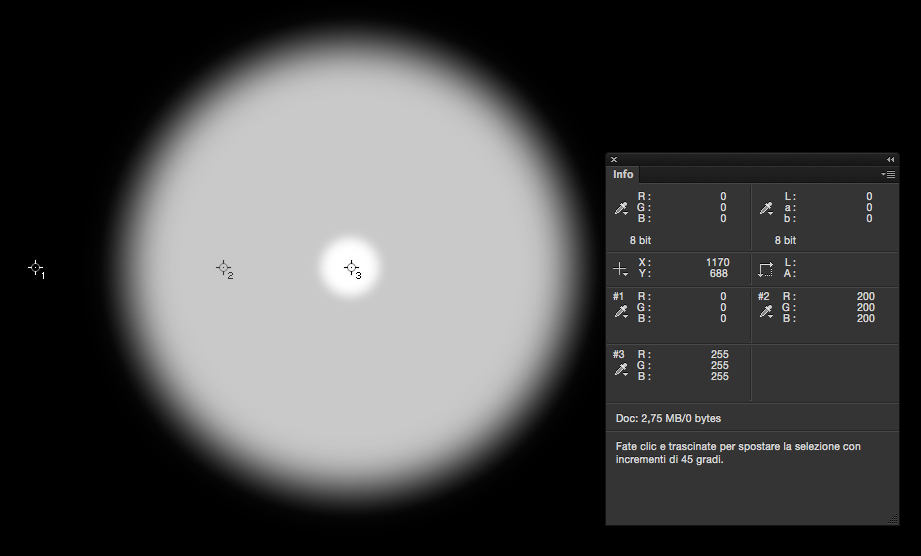
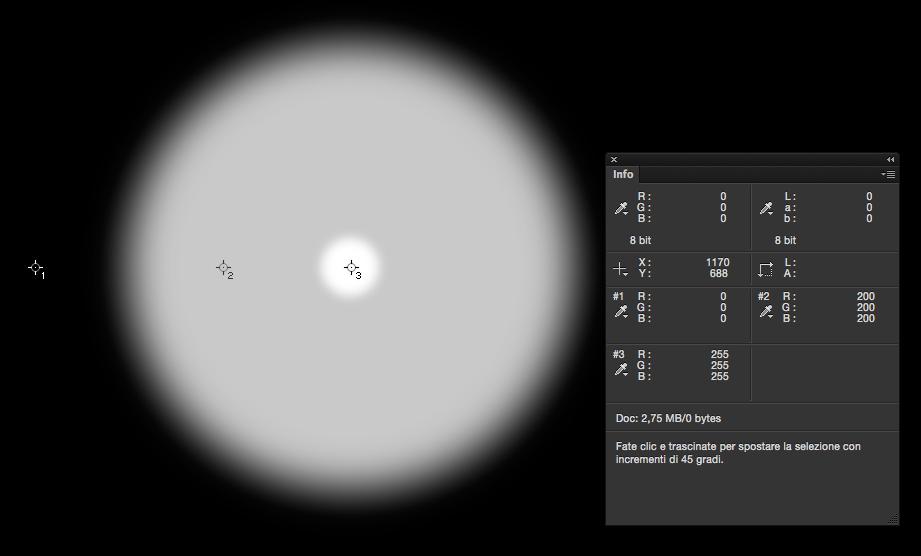
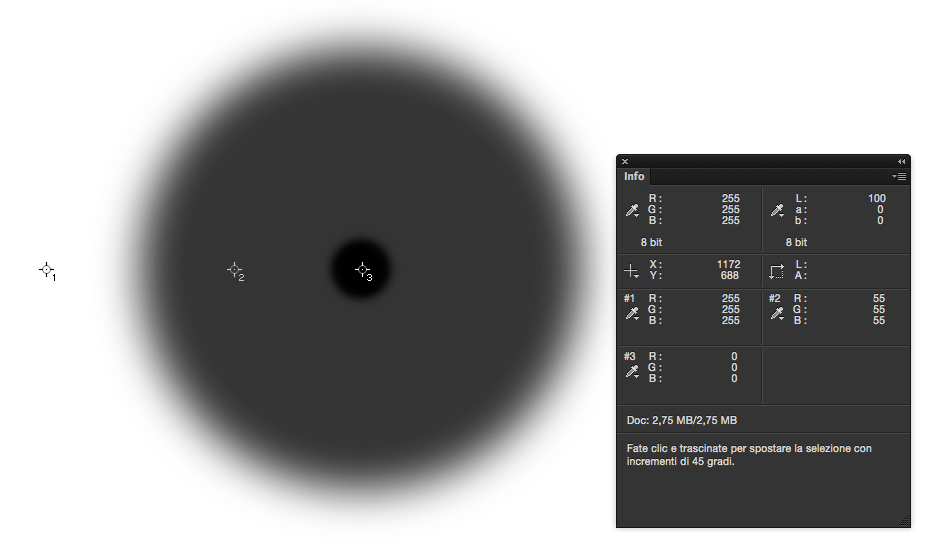
Per esemplificare riporto i risultati dell’appello campionando tre pixel corrispondenti rispettivamente allo sfondo nero (tutti assenti), alla parte grigia e uniforme del cerchio (200 presenti) e alla parte centrale bianca (tutti presenti, 255).

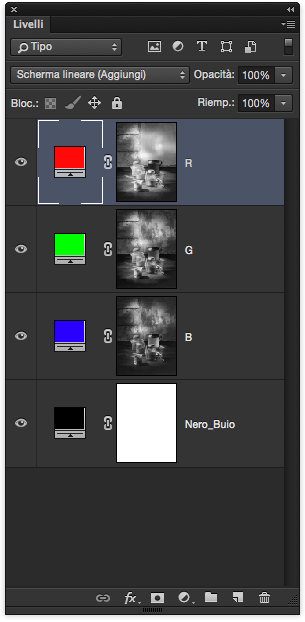
Per rendere più evidente l’operazione aggiungo il livello che rispecchia la registrazione del sensore in  un livello separato, “Positivo”, al quale applico il MDF (metodo di fusione)  Scherma lineare (Aggiungi).

Così facendo i valori registrati dal sensore vengono “aggiunti” al livello di sfondo.  Rispetto al MDF Normale in questo caso non cambia niente, ma Aggiungi rispecchia la logica dell’operazione e ci sarà utile quando proveremo con un’immagine a colori.

Otteniamo in tal modo una riproduzione dell’immagine originale.

Le cose richiedono un po’ più di attenzione se il conteggio avviene in negativo.

L’insegnante in questo caso immagina che tutte le classi siano al completo, 255 microstudenti luminosi per ciascun pixel. Lo sfondo bianco rappresenta questa improbabile situazione con tutte le classi piene.

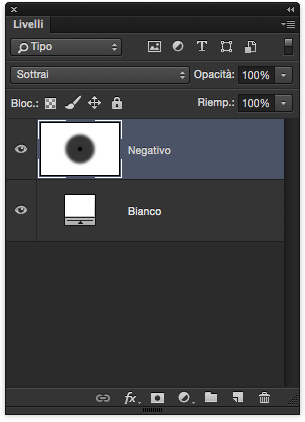
Dopo il conteggio degli assenti, l’elenco che li rappresenta è raffigurato dall’immagine in negativo sotto riprodotta. (È l’immagine dei fotoni rimasti a casa. ).

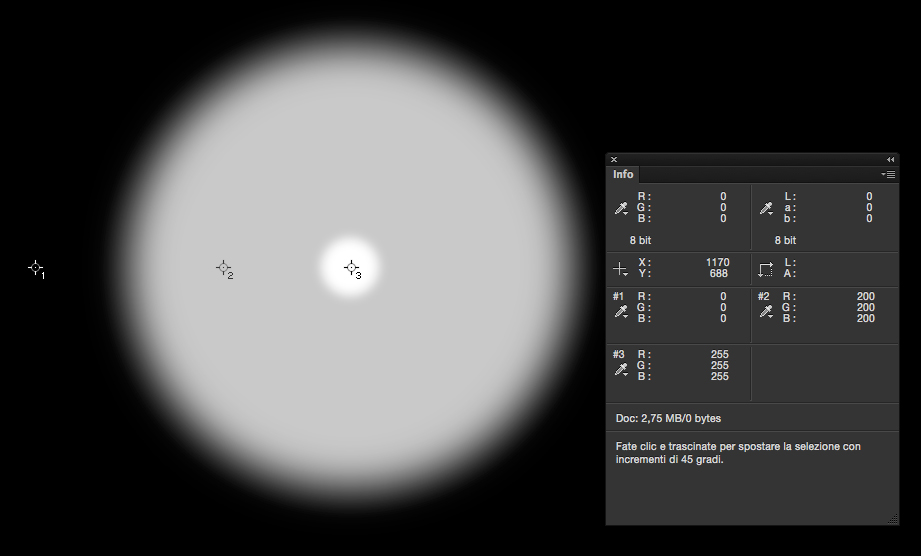
Dove prima contavamo zero Fotoni per pixel/classe (il nero) ora contiamo i fotoni assenti, 255, che insieme danno il bianco. Dove prima contavamo 200 Fotoni presenti, il grigio chiaro, ora contiamo gli assenti, 55, rappresentati da un grigio scuro. Dove prima contavamo la classe al completo, 255, il bianco, ora contiamo gli assenti, nessuno, rappresentati dal nero.

 

Non ci resta che sottrarre gli assenti  (il negativo) all’elenco di tutti gli iscritti  (lo sfondo bianco).

La disposizione dei livelli e il MDF Sottrai mostrano proprio questa operazione: sottrai gli assenti dall’elenco completo.

Otteniamo in tal modo, di nuovo, un risultato identico all’originale.

Pensiamo all’immagine ottenuta grazie a una diapositiva.

Nel primo esempio, quello della sintesi additiva, con Aggiungi simuliamo la proiezione su uno schermo ponendo l’attenzione alla trasparenza della diapositiva, a quanti fotoni vengono lasciati passare, in una scala da 0 a 255, per illuminare lo schermo.

Nel secondo caso, in sintesi sottrattiva, è più facile se immaginiamo di visionare la diapositiva su un tavolo luminoso e poniamo l’attenzione all’opacità della diapositiva, a quanti fotoni sono sottratti,  da 0 a 255, alla luce bianca.

In fisica, l’opacità è l’opposto della trasparenza e i due valori sono strettamente collegati, come è facile capire da questi esempi.

Passiamo ora a un’immagine a colori. Per semplicità evitiamo anche in questo caso problemi di demosaicizzazione e immaginiamo di scattare con una fotocamera dotata di un dorso a scansione che possa registrare la componente rossa, quella verde e quella blu nello stesso pixel.

Le microclassi al completo saranno allora composte da 255 x 3 = 765 microscopici studenti colorati e luminosi. 255 rossi, 255 verdi e 255 blu.

Ok, forse è ora di abbandonare l’analogia con gli studenti lillipuziani.

Cosa succede se fotografiamo un soggetto a colori? Analogamente a quanto visto prima, il sensore registrerà, per ogni singolo pixel, la presenza dei Fotoni, questa volta considerando anche la lunghezza d’onda della luce incidente. Ovvero, per usare un termine improprio, il suo colore.

Prendiamo un soggetto semplice e astratto come quello sotto riprodotto.

Vogliamo ora riprodurre l’immagine registrata dal sensore secondo i principi della sintesi additiva. Un solo proiettore non ci basta, nella maggior parte dei casi. Dobbiamo immaginare di averne 3, dotati di illuminanti rossi, verdi e blu rispettivamente.

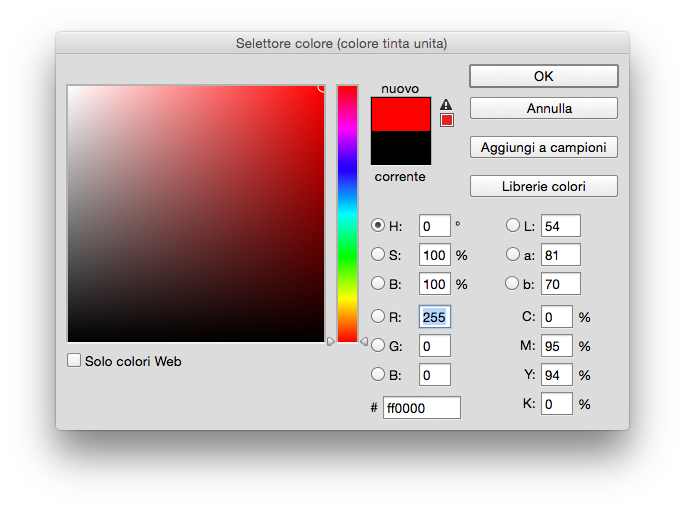
Ma come scegliamo questi tre colori, in Photoshop? Nella simulazione dell’illuminante di ciascuno dei primari ho utilizzato dei livelli di riempimento:

Livello -> Nuovo livello di riempimento -> Tinta unita

scegliendo per ogni primario il massimo valore, ovvero la massima intensità luminosa possibile del proiettore corrispondente. In questo modo avremo un rosso, un verde e un blu con caratteristiche ben definite dal profilo colore che stiamo adottando: Adobe RGB, sRGB o altro.

Nell’immagine sotto la selezione del colore Rosso.

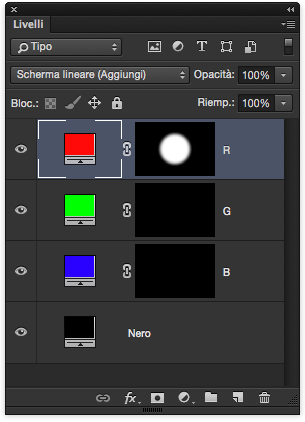
Il pannello Livelli riportato sotto mostra la simulazione di quanto avviene in sintesi additiva.

Lo sfondo simula la situazione di partenza, il buio. Lì si trova lo schermo di proiezione; lì sono diretti i tre proiettori colorati.

Il livello più alto corrisponde all’illuminante rosso. La maschera di livello simula la diapositiva che limita la proiezione del fascio di luce. Il nero è la parte opaca della diapositiva, dove la luce viene bloccata;  il bianco corrisponde alla trasparenza, dove la luce viene trasmessa.

Il secondo livello corrisponde al faretto verde. Tutta la luce viene schermata. Anche nel terzo faretto, quello blu, tutta la luce viene schermata.

Sotto, il risultato dell’effetto dei singoli livelli/faretti.

Il risultato finale riproduce, per sintesi additiva, l’immagine originale.

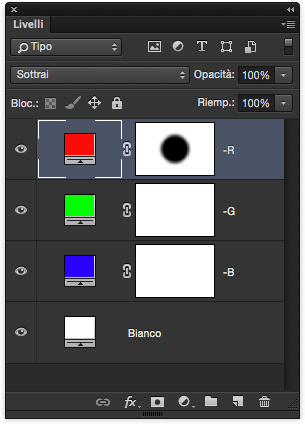
Proviamo ora ad operare per sottrazione. Dobbiamo cambiare prospettiva. Lo sfondo, che ora è bianco, non corrisponde più allo schermo di proiezione ma è il bianco del proiettore senza filtri (o del tavolo luminoso, se vi risulta più semplice).

Un unico proiettore che irradia luce bianca: i livelli colorati al di sopra, dunque, corrispondono ora a dei filtri che sottraggono i colori corrispondenti e le maschere sono il negativo delle precedenti.

Il livello più alto sottrae il rosso ovunque tranne nella parte centrale dove la maschera è nera a significare che il filtro in quell’area è perfettamente trasparente. E di che colore apparirebbe la luce bianca se ad essere sottratta fosse la sola componente rossa? Ai nostri occhi continuerebbero ad arrivare la componente verde e quella blu, e quindi la luce ci apparirebbe ciano. Ma il secondo livello sottrae il verde su tutta l’immagine. E il terzo sottrae la componente blu.

Sotto, il risultato delle sottrazioni del Rosso, del Verde e del Blu operata da filtri ideali. Come si può vedere, alla luce bianca vengono sottratte le componenti R, G e B ovunque, tranne nella parte centrale dell’immagine dove la sola componente rossa viene risparmiata.

Il risultato della sottrazione, almeno nella simulazione teorica che non si scontra con le problematiche tecnologiche relative alle curve di trasmissione dei filtri, è dunque identico a quello ottenuto in positivo, per addizione.

Bianco meno R, corrisponde naturalmente al Ciano; bianco meno G al Magenta e bianco meno B al Giallo.

Vorrei a questo punto porre una domanda. Abbandoniamo per un attimo Photoshop e ammettiamo che una delle due simulazioni appena descritte si realizzi davvero nella sala buia di un cinema.

Noi siamo gli osservatori e possiamo guardare solamente lo schermo davanti a noi, senza sapere se quanto stiamo osservando è il risultato di una delle possibili combinazioni  con l’uso di tre luci colorate o il risultato della sottrazione, alla luce bianca, di alcune componenti cromatiche ad opera di filtri ciano, magenta e giallo.

Vedremmo qualcosa di diverso nei due casi?

Sarebbe in qualche modo diversa la luce che andrebbe a colpire la nostra retina?

Lascio la domanda senza risposta. Personalmente ho un’opinione piuttosto precisa a riguardo. Per averne discusso in passato so però che persone autorevoli hanno un’opinione opposta alla mia, ma sinceramente non sono riuscito a capirla. Se qualcuno può aiutarmi, sono sempre pronto a cambiare le mie convinzioni e a ringraziare chi mi farà capire qualcosa di nuovo.

Poiché ritengo che il quesito posto sia piuttosto importante, provo a esemplificarlo con l’aiuto di alcune immagini.

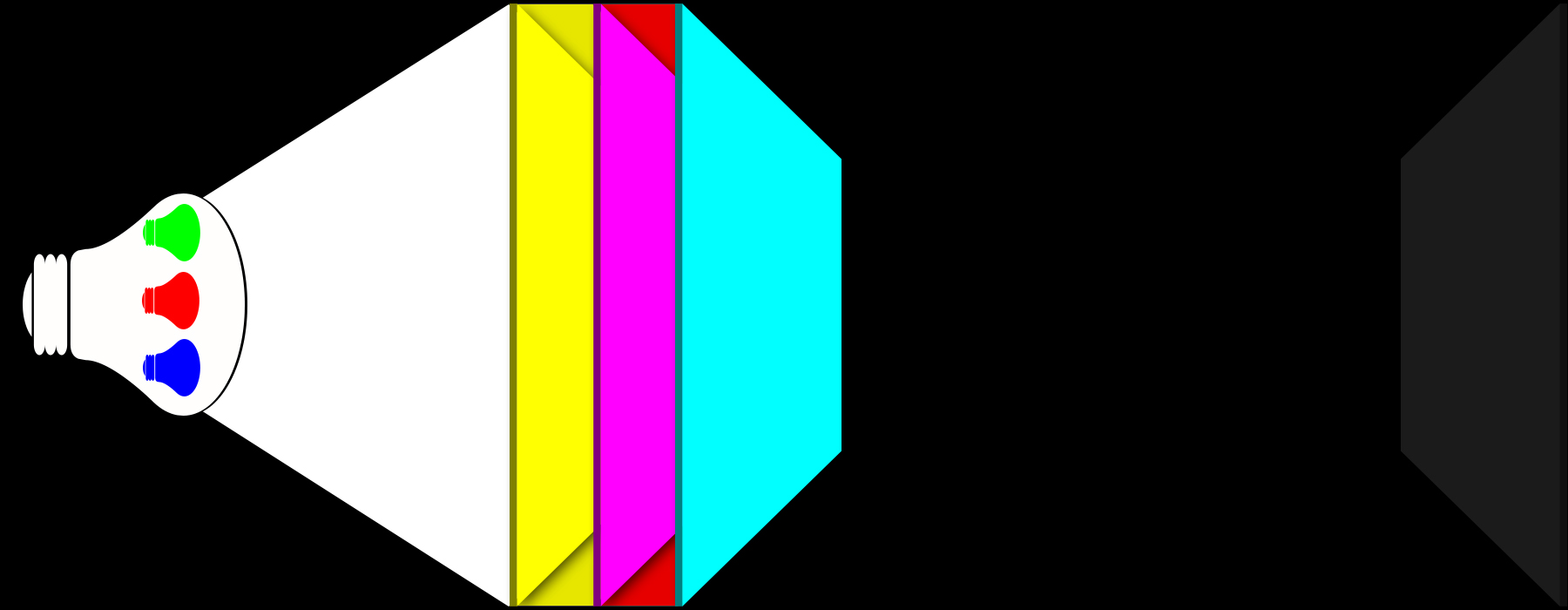
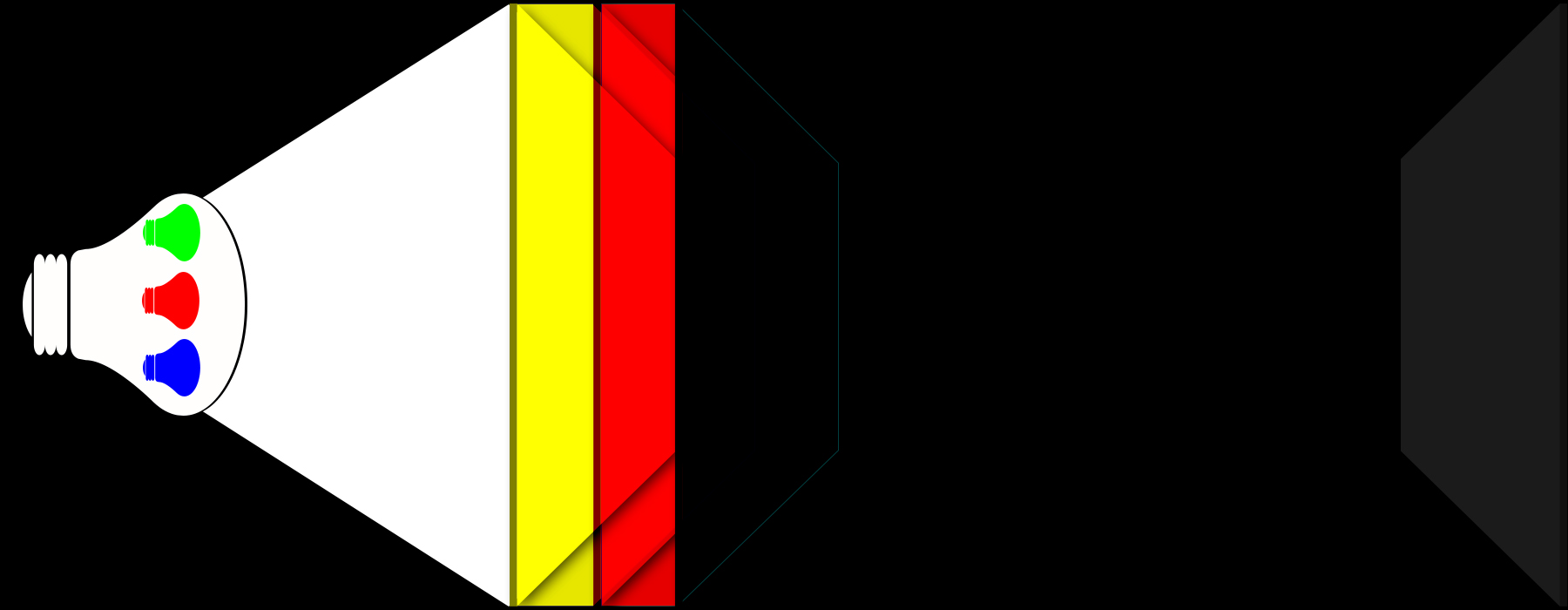
La prima simula la proiezione di una lampadina bianca che proietta la sua luce verso uno schermo e la cui luce è filtrata da tre filtri, uno giallo uno magenta e uno ciano.

Ho immaginato la lampadina fatta di un vetro opalino bianco all’interno della quale ci sono tre piccole lampadine, una “verde”, una “rossa” e una “blu” che insieme irradiano le diverse lunghezze d’onda che formano il bianco.

I filtri sono quelli che alla fine del processo di sviluppo si formano in una diapositiva analogica. Il filtro giallo raggiunge la massima saturazione dove la pellicola non è stata impressionata dalla luce blu, il filtro magenta la raggiunge dove non è stato impressionata dalla luce verde e quello ciano dove non è stato impressionata dalla luce rossa. Dove invece le lunghezze d’onda relative al blu, al verde e al rosso hanno impressionato i corrispondenti strati di pellicola destinati al colore complementare, abbiamo un proporzionale aumento della trasparenza dei filtri stessi.

Dunque, per la sintesi sottrattiva consideriamo questa immagine.

 

A dire il vero non è molto fedele, in quanto per effetto della posizione dei filtri una rappresentazione più corretta sarebbe quella dell’immagine qui sotto.

 

Infatti, dalla sovrapposizione di giallo e magenta otteniamo il rosso. Dove si sovrappongono giallo, magenta e ciano abbiamo il nero.

La rappresentazione è quindi più corretta ma fa perdere di vista quali sono i filtri che stiamo utilizzando. Trascurerò quindi questo aspetto e continuerò a rappresentare i filtri come nella prima figura.

In questa prima situazione la luce bianca della lampada viene prima filtrata dal filtro giallo che assorbe la componente blu. Poi, il filtro magenta assorbe la componente verde. Resta solo la componente  rossa che è però assorbita dal filtro ciano.

Lo schermo rimane dunque nero.

Questo è il risultato che otterremmo sviluppando una diapositiva senza esporla.

Ma cosa sarebbe successo se avessimo fotografato una parete rossa?

In quel caso, alla fine del processo di sviluppo lo strato di pellicola sopra rappresentato in ciano sarebbe perfettamente trasparente, come nell’immagine sotto.

Nell’esempio sulla sintesi sottrattiva ho fatto riferimento a dei filtri posti davanti a un proiettore.

In quel caso lo schermo di proiezione apparirebbe rosso.

E se fosse trasparente anche lo strato intermedio?

La luce sarebbe filtrata dal solo filtro giallo ed è di questo colore che apparirebbe anche lo schermo di proiezione.

Ma proviamo ora ad eliminare la parte esterna della lampada e tenere solo le componenti interne, la lampadina verde, quella rossa e quella blu.

Ed eliminiamo pure i filtri. Siamo ora in sintesi additiva.

Lo schermo sarebbe illuminato dalle tre componenti cromatiche e apparirebbe bianco.

Per simulare la situazione da cui siamo partiti, lo schermo nero, dobbiamo spegnere le tre lampadine.

Ho lasciato un minimo di visibilità alle tre lampadine solo per ricordare che ci sono, ma immaginiamole spente.

Apparirebbe diverso lo schermo di proiezione rispetto al primo caso visto in sintesi sottrattiva? Con la lampada accesa e i tre filtri alla massima saturazione?

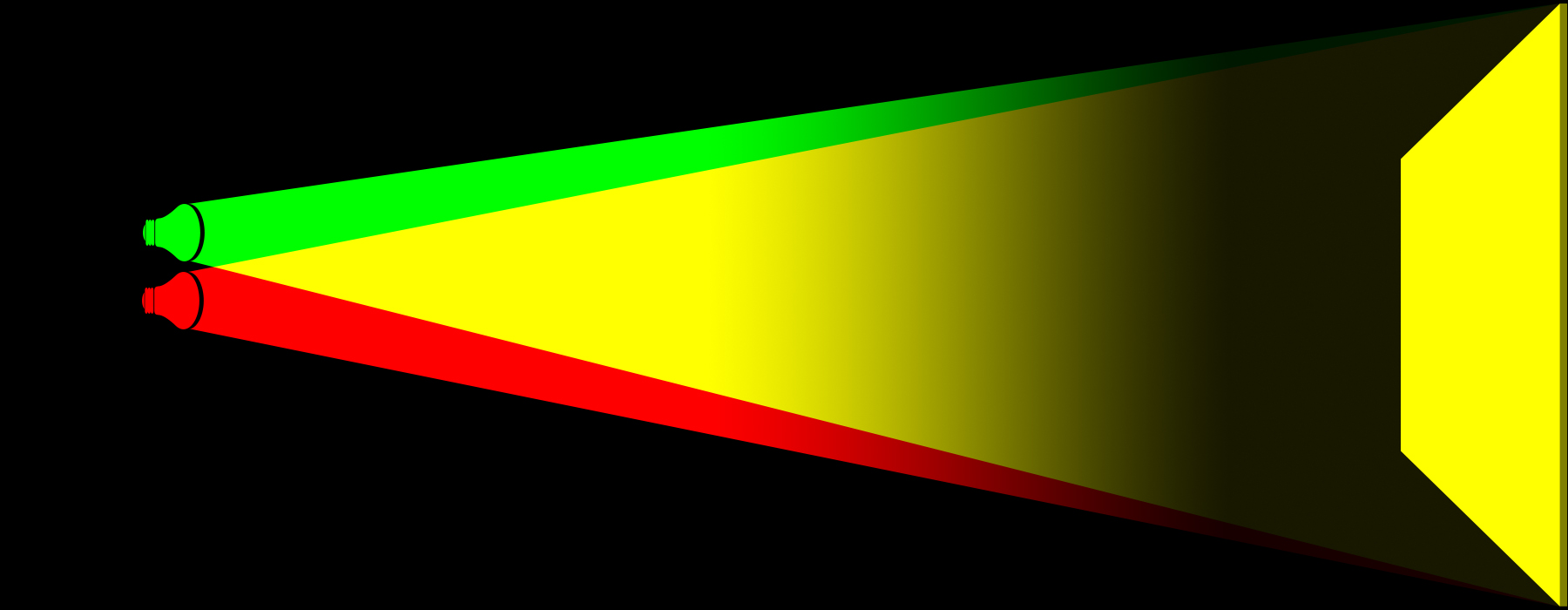
Proviamo a simulare il secondo caso, quando in sintesi sottrattiva abbiamo considerato il filtro ciano perfettamente trasparente.

Per farlo accendiamo la lampadina rossa.

Pensate che sarebbe possibile, guardando lo schermo, sapere in quale delle due possibilità proposte ci stiamo trovando?

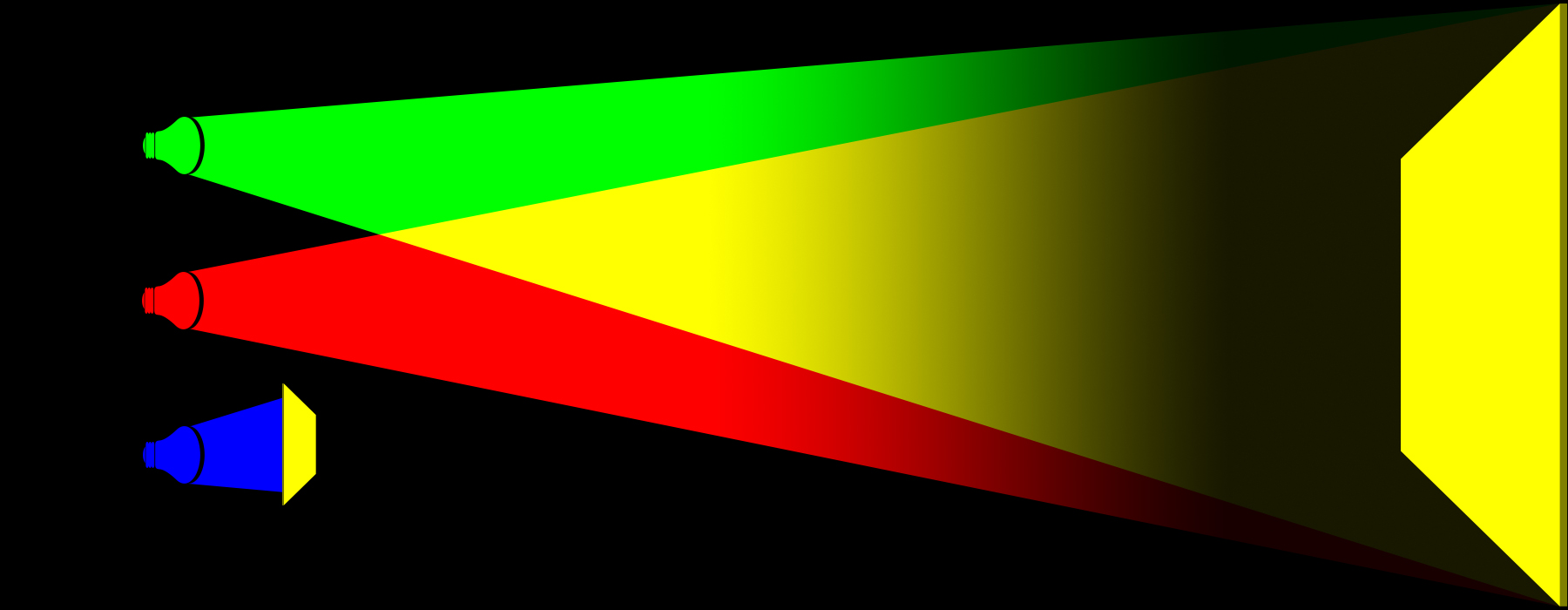
Infine simuliamo l’ultimo caso visto per la sintesi sottrattiva, quello che vedeva la presenza del solo filtro giallo.

Per farlo, aggingiamo la luce verde alla rossa.

Ancora una volta, lo schermo rifletterebbe qualcosa di diverso?

Abbiamo considerato essenzialmente due modi per creare i colori. Nel primo le luci sono accese e il flusso delle diverse componenti cromatiche viene selettivamente limitato da appositi filtri.

Nel secondo abbiamo “acceso” solo le lampadine che volevamo.

Vediamo una terza situazione: quella che vede le lampadine corrispondenti alle tre componenti cromatiche sempre accese e abbinate ai loro filtri complementari.

Siamo in una situazione molto simile a quella precedente; i filtri sono semplicemente un modo per controllare l’intensità della luce che arriva sullo schermo da ogni singola lampadina. Con il filtro perfettamente trasparente abbiamo la massima intensità, con il filtro alla massima densità tutta la luce di una specifica sorgente viene bloccata ed è come se la lampadina fosse spenta.

Ecco che questa immagine riproduce il primo caso.

Ho semplicemente distanziato le lampadine e rimpicciolito i filtri, per motivi grafici. Ma consideriamo siano le stesse lampadine considerate finora, accese e abbinate ai filtri complementari, gli stessi già usati sovrapposti e che ora usiamo in modo separato.

Se i filtri sono perfetti, assorbono la luce complementare, riproducendo una situazione già vista, di buio. Sarà un buio diverso?

E per vedere lo schermo rosso? Ci basterà togliere il filtro ciano, abbinato alla luce rossa.

Lo schermo ci apparirebbe di un rosso diverso rispetto ai due precedenti modi usati per ottenere il rosso?

E per il giallo? Togliamo il filtro magenta, abbinato alla luce verde e quello ciano, abbinato alla luce rossa.

Percepiremmo un giallo diverso rispetto alle situazioni già viste?

Ho fatto questi esempi pensando a chi, come me, è cresciuto con la fotografia analogica e ricorda bene le diapositive in telaietto perché ha assistito a parecchie proiezioni. Le diapositive erano posizionate in un carrello e venivano meccanicamente inserite all’interno di un proiettore. La luce bianca del proiettore subiva in tal modo una sottrazione cromatica selettiva proporzionale alle densità dei tre filtri, giallo, magenta e ciano, che costituivano l’essenza della diapositiva stessa.

Un altro esempio di sintesi sottrattiva è quello della stampa che utilizza inchiostri ciano, magenta e giallo. Sono questi gli inchiostri che consentono di regolare, per sottrazione, le componenti rossa, verde e blu dell’immagine nella stampa in quadricromia che vede anche l’aggiunta dell’inchiostro nero.

Per essere precisi, per motivi legati alla tecnologia usata, in stampa gli inchiostri sono depositati sulla carta sempre al massimo della saturazione ma in punti di dimensioni diverse, lasciando tra i punti stessi dei vuoti. In queste aree non inchiostrate appare il fondo della carta, che contribuisce per via additiva (e non sottrattiva, come spesso si sottintende!) alla saturazione e alla luminosità del colore. Così, un magenta molto saturo sarà costituito da punti d’inchiostro magenta depositati in modo da lasciare vedere poco del fondo della carta. Mentre gli spazi bianchi saranno molto più estesi in corrispondenza di un magenta poco saturo.

La curva di assorbimento degli inchiostri reali si differenzia da quella ideale e bisogna tenerne conto. In particolare, l’inchiostro ciano è un inchiostro debole ed è il motivo per il quale ne serve percentualmente di più.

La logica rimane comunque quella già considerata. Rivediamola ora applicata ad un’immagine fotografica. L’immagine è un mio vecchio scatto, per un calendario del 1998, frutto della collaborazione con con l’art director Riccardo Ruffo, quando collaboravo come fotografo con lo studio “Lineagrafica”. Per tema, quel calendario aveva “I colori”, una mia proposta. 🙂

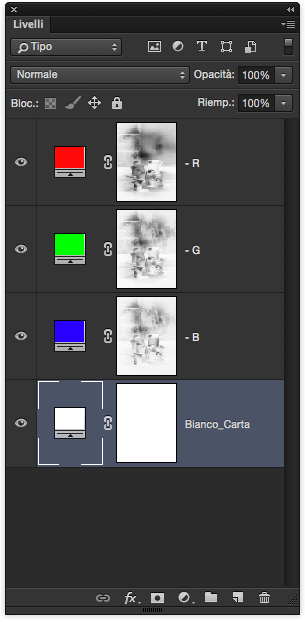
La disposizione dei livelli che simulano quanto succede secondo il principio della sintesi additiva è riportata sotto. Come si vede dalle maschere, la ricostruzione dell’immagine avviene in positivo, per addizione.

Per chi volesse seguirmi nella simulazione, le maschere sono state ottenute applicando i canali corrispondenti dell’originale, che ho poi eliminato, alle maschere di ciascun primario simulato con i livelli di riempimento.

Riporto anche il risultato delle singole proiezioni. Quella del rosso, quella del verde e quella del blu che insieme ricostruiscono l’immagine originale.

Tra parentesi ricordo che era essenzialmente questa la tecnica realizzata per riprodurre le prime proiezioni a colori.

Vediamo ora la disposizione dei livelli che simula la ricostruzione dell’immagine per sottrazione.

Le maschere sono in negativo.

Il Rosso, il Verde e il Blu vengono sottratti nei rispettivi canali. La sottrazione avviene dal bianco. Si può pensare all’effetto di inchiostri perfetti depositati sulla carta.

Riporto i risultati delle singole sottrazioni.

Finora abbiamo simulato sia i risultati in positivo sia quelli in negativo rimanendo in RGB, a dimostrazione del ruolo fondamentale di questi tre primari.

Ma per riprodurre la sintesi sottrattiva è più coerente cambiare metodo di lavoro.

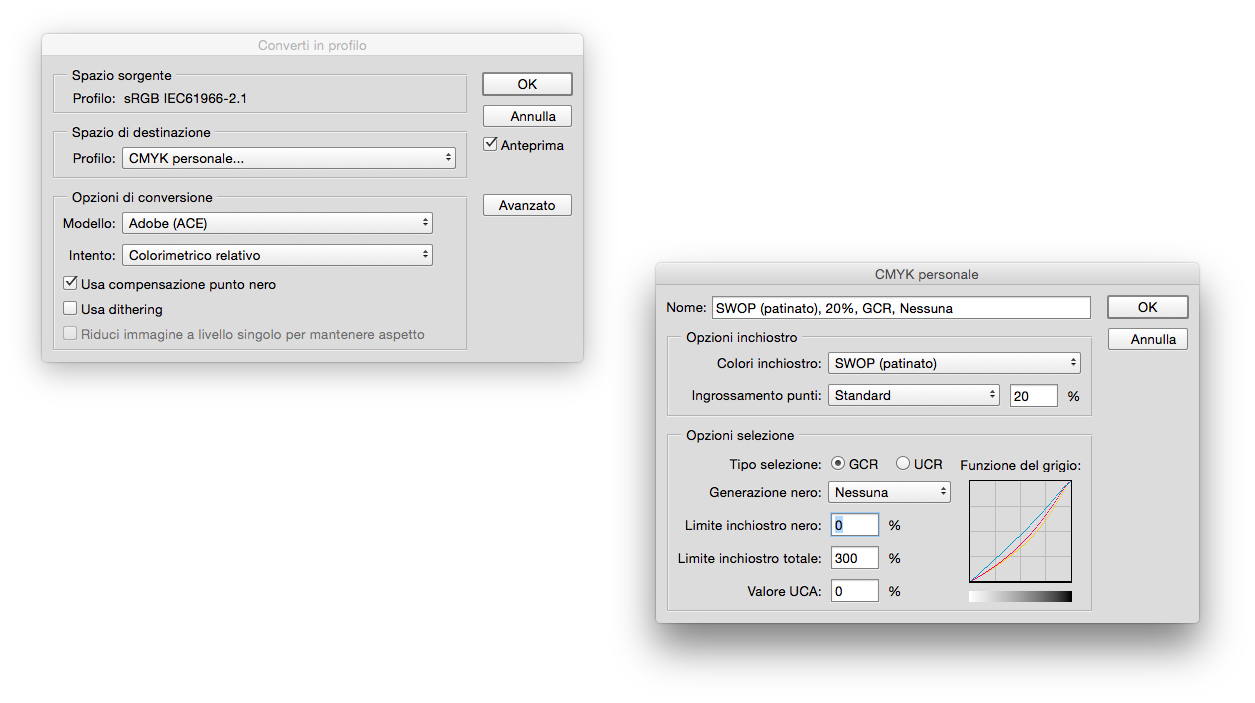
Trasferiamoci quindi in CMYK: Immagine -> Metodo -> CMYK.

Come abbiamo fatto per la sintesi additiva, scegliamo di simulare i primari con dei livelli di riempimento:

Livello -> Nuovo livello di riempimento -> Tinta unita

impostando questa volta i valori nelle caselle che fanno riferimento alla sintesi sottrattiva.

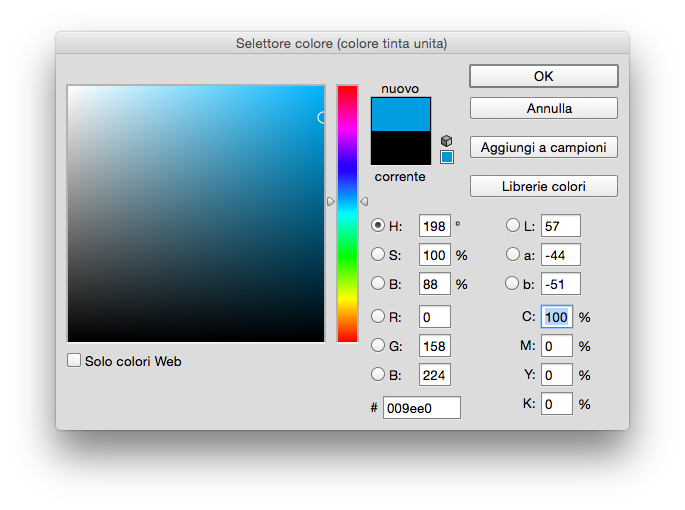
Nell’immagine sotto la selezione del colore Ciano.

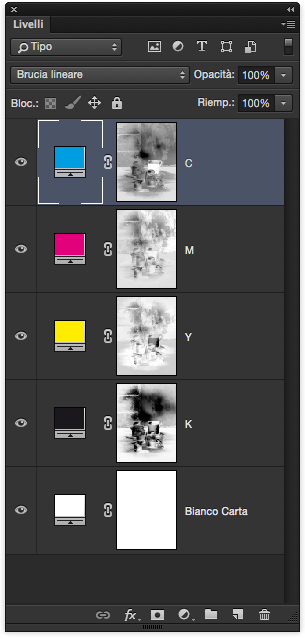
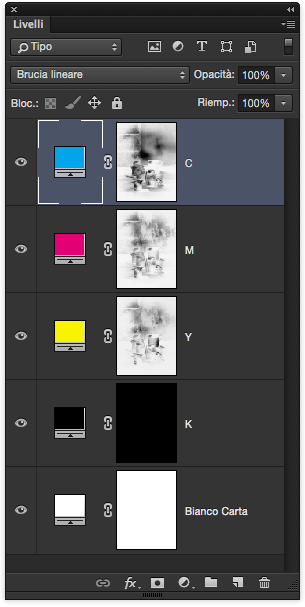
Nella disposizione dei livelli vediamo l’uso degli inchiostri Ciano, Magenta, Giallo e anche del nero.

Il metodo di fusione Brucia Lineare simula la sovrapposizione di filtri colorati.

Dire che stiamo usando il colore ciano in brucia lineare equivale a dire che stiamo sottraendo il suo complementare, il rosso.

Stessa logica per il Magenta con il verde e del giallo con il blu.

Il nero è un inchiostro acromatico che va a sostituire una combinazione neutra di Giallo, Magenta e Ciano. Per questo motivo i canali CMY sono più leggeri dei corrispettivi canali -R, -G e -B già visti dove non avevamo il nero.

L’aspetto dei canali CMYK.

Ed ecco il risultato finale ottenuto per sottrazione di R, ad opera di C, di G, ad opera di M e di B ad opera di Y. Con l’aggiunta del nero.

Ma avremmo potuto ottenere il medesimo risultato senza il nero?

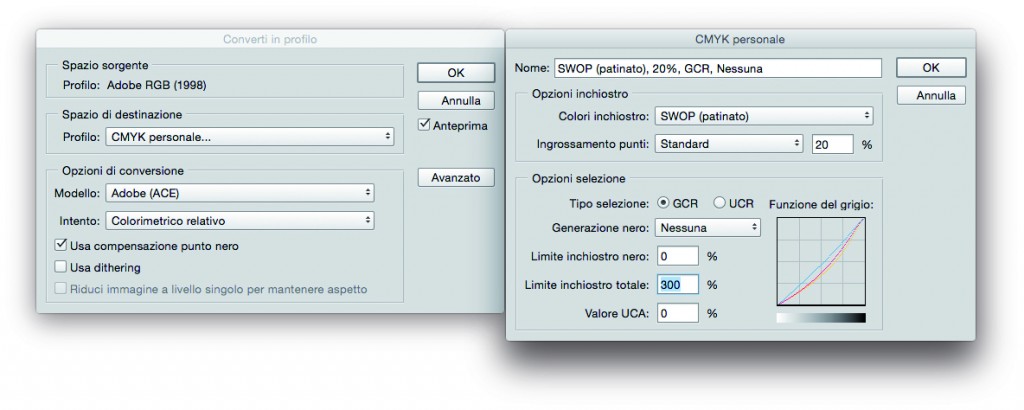
Photoshop consente una conversione personale in CMYK, dove abbiamo la possibilità di scegliere tra diverse possibilità di generazione del nero: nessuna, bassa, alta, media e massima.

Il GCR si basa quindi sulla sostituzione di una parte della componente grigia (Gray Component Replacement).

Se scegliamo Nessuna interverranno solo gli inchiostri CMY.

La palette dei livelli mostra la mancata generazione del canale del nero.

L’aspetto dei canali è quindi quello sotto riportato, dove ciascun canale cromatico è più carico di inchiostro ma manca il nero.

A questo punto è utile un confronto tra l’aspetto dei canali con e senza generazione del nero. Dall’immagine si vede che i canali cromatici si vede che quelli che derivano da una conversione senza GCR sono più carichi, ma non di molto in quanto gli inchiostri non possono andare, ciascuno, oltre alla copertura del 100%.

In un’immagine scura come questa non riescono pertanto a compensare l’assenza del nero.

Le parti più scure non possono andare infatti globalmente oltre il 300%, mentre con la presenza dell’inchiostro nero si può andare oltre. Oppure ottenere neri più profondi rimanendo negli stessi limiti.

Sotto, la finestra che permette di impostare il limite d’inchiostro.

Nel confronto tra i due risultati finali si vede come l’assenza dell’inchiostro nero comporti un’immagine con neri meno profondi.

L’inchiostro nero è dunque una componente fondamentale per costruire l’immagine in quadricromia.

In una situazione ideale, con inchiostri ciano, magenta e giallo ideali, ovvero capaci di assorbire completamente i rispettivi complementari rosso, verde e blu, il nero non sarebbe indispensabile. Ma nel mondo reale il nero serve e la sua funzione principale è quella di assorbire parti uguali di R, G e B compensando i limiti degli inchiostri cromatici. Inoltre, il nero porta ad un risparmio complessivo di inchiostri e evita i problemi di registro dove viene usato il nero pieno, per esempio nelle scritte.

[Nota di MO: vale la pena sottolineare che la presenza dell’inchiostro nero ha essenzialmente la funzione di aumentare il gamut disponibile in stampa. Spesso quando si parla di gamut “ampio” ci si riferisce a spazi colore in grado di riprodurre colori saturi e brillanti. Sono indubbiamente importanti, anche perché sono difficili se non impossibili da riprodurre; ma esiste anche un gamut sul versante opposto, quello dei colori scuri e desaturati. Uno dei ruoli dell’inchiostro nero è espandere il gamut in quell’area.]

In questo articolo ho voluto mantenere l’attenzione a come vengono controllati il rosso, il verde e il blu nella formazione delle immagini.

Sia la sintesi additiva sia la sintesi sottrattiva sono state esposte alla luce di RGB.

Ho usato livelli di riempimento, maschere di livello e metodi di fusione perché credo che in tal modo si riesca a mostrare più chiaramente come funzionano i canali in sintesi additiva e in sintesi sottrattiva.

Il mio obiettivo principale è però quello di capire un po’ meglio come funziona Lab.

Lo farò prossimamente, cercando di seguire la stessa logica usata in questo articolo.