Nello scorso mese di gennaio Francesco Marzoli ha pubblicato un’interessante domanda sul gruppo CCC presente su facebook. Ho avuto in mente di scriverne per circa tre mesi e ora è giunto il momento di farlo, recuperando alcuni appunti che avevo messo assieme subito dopo il suo post. Partiamo dalla domanda originale, leggermente riformulata:
Aprite la stessa immagine a 16 bit e a 8 bit, nella regolazione Livelli comprimete i livelli di output a 120 e 136, successivamente riaprite Livelli e cliccate su automatico. Perchè l’immagine a 16 bit torna in originale?
Ho fatto alcune prove per capire bene cosa succede in realtà e vorrei condividere i risultati con voi.

Partiamo dall’immagine su cui lavoreremo. Si tratta di un semplice ritratto senza particolari pretese. Lo scatto è stato effettuato con una Canon 40D in formato raw e sviluppato in Adobe Camera Raw. Non sono state effettuate operazioni in Photoshop, salvo un ridimensionamento al 25% dell’originale dopo l’apertura. Lo sviluppo, in questo caso, è stato effettuato convertendo l’immagine in sRGB a 8 bit: un’immagine come questa non ha probabilmente bisogno di spazi colore più estesi.
Facciamo ora il nostro esperimento, modificando leggermente il flusso di lavoro suggerito da Francesco Marzoli per ottenere dei risultati più coerenti. Potete provare anche voi su un’immagine qualsiasi, anche se è meglio utilizzare un’immagine in cui ci siano variazioni non selvagge ma significative dei toni e della luminosità – come nel caso del viso in questa fotografia. In questa specifica immagine il contrasto è già praticamente massimizzato, ma in altre immagini le cose non vanno necessariamente così. A causa di questo fatto aggiungiamo al flusso di lavoro suggerito un’operazione di massimizzazione del contrasto preliminare.
- Aprite l’immagine in Photoshop. Per semplicità, ipotizzeremo che sia composta da un solo livello.
- Aprite la regolazione Livelli (Menu Immagine -> Regolazioni -> Livelli…, o se preferite cmd-L, o ctrl-L se lavorate su PC).
- Cliccate sul pulsante Opzioni.
- Nella sezione Algoritmi, selezionate Migliora contrasto monocromatico.
- Cliccate sul pulsante OK, prima nella finestra Opzioni e poi in quella principale.
- Duplicate il livello corrente (Menu Livello -> Duplica livello…, o se preferite cmd-J, o ctrl-J se lavorate su PC).
- Aprite di nuovo la regolazione Livelli.
- Digitate rispettivamente 120 e 136 nelle due caselle in basso sotto la dicitura Livelli in output e cliccate sul pulsante OK:
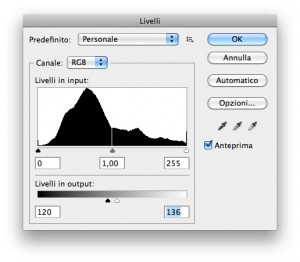
Digitate 120 e 136 come minimo e massimo livello di output, rispettivamente. - In questo modo ottenete una versione dell’immagine estremamente poco contrastata:

Il risultato dell’enorme compressione dei livelli in output. - Aprite di nuovo la regolazione Livelli.
- Cliccate sul pulsante Opzioni.
- Nella sezione Algoritmi, selezionate Migliora contrasto monocromatico.
- Cliccate sul pulsante OK, prima nella finestra Opzioni e poi in quella principale.
L’immagine che otterrete è piuttosto atroce: una posterizzazione fortissima si è venuta a creare in diverse zone, a seconda della loro natura e della loro struttura di luminosità (cliccate sull’immagine per una versione ingrandita). Ora, ripartendo dal file raw e utilizzando gli stessi parametri effettuate uno sviluppo a 16 bit e ripetete esattamente la stessa procedura. Sorpresa: il risultato che ottenete è identico all’originale, ovvero non presenta la posterizzazione che abbiamo invece riscontrato nell’immagine a 8 bit. In realtà una minima differenza esiste, ma è troppo piccola per essere riscontrata a occhio, a meno che non andiate a osservare delle aree critiche a un ingrandimento del 100%, e anche in quel caso si tratterà con ogni probabilità di una differenza assolutamente irrilevante. Di questo parleremo a breve, perché – anticipando qualcosa che spiegherò tra poco – la procedura che abbiamo usato è in realtà errata e non fa ciò che ci aspetteremmo a causa di una caratteristica poco nota di Photoshop che andremo a discutere.
In generale il fatto che le immagini a 16 bit si compromettano meno di quelle a 8 bit viene utilizzato in media per dimostrare la superiorità del formato a 16 bit. In parte questa conclusione è vera: ma va presa con le pinze, come qualsiasi conclusione assoluta. Qui di seguito vorrei discutere il perché di questa mia affermazione.
Cerchiamo innanzitutto di capire in cosa consiste questa procedura. Inizialmente effettuiamo un’operazione di contrasto automatico per massimizzare il range della luminosità dell’immagine secondo un qualche algoritmo. La nostra scelta (Migliora contrasto monocromatico) ci fornisce l’immagine più contrastata compatibile con il colore attuale dell’immagine (ovvero con i rapporti tra i canali R, G e B) senza che si presenti clipping. In altri termini, il canale composito RGB (Luminosità) massimizza il suo range senza che necessariamente R, G e B siano massimizzati separatamente.
Ricordiamo innanzitutto che in un’immagine a 8 bit codificata nel metodo colore RGB tutti i canali possono assumere solo valori compresi tra 0 e 255. Quando andiamo a comprimere i livelli in output facciamo essenzialmente questo:
- I pixel la cui luminosità è pari a 0 vengono mappati a 120.
- I pixel la cui luminosità è pari a 255 vengono mappati a 136.
Questo spiega perché il contrasto dell’immagine compressa diventa bassissimo: il punto d’ombra assume valori ridicolmente alti, quello di luce altrettanto ridicolmente bassi. Tutti i punti intermedi vengono schiacciati all’interno di questo intervallo, e dunque addio contrasto. I numeri 120 e 136 non sono scelti a caso: ma per comprenderlo dobbiamo ragionare in termini di 16 bit, anche se purtroppo c’è una complicazione che dobbiamo affrontare. In ogni caso, in 8 bit si passa da un’immagine che ha 256 livelli di luminosità a una che ne ha soltanto 16. Questo perché il range dinamico massimo è dato da 136 – 120 = 16.

La posterizzazione deriva proprio da questa riduzione dei livelli di luminosità. Facciamo i conti: tutta l’immagine viene divisa in sedici livelli soltanto; questo significa che tutti i valori originali compresi tra 0 e 15 vengono mappati a 120; tutti quelli compresi tra 16 e 31 vengono mappati a 121; quelli compresi tra 32 e 47 a 122, e via dicendo. I numeri di per sé non sono importanti: è importante comprendere che dopo la compressione dei livelli in output ci ritroviamo con una “scalinata” di soli 16 livelli di grigio in ogni canale. Questo è chiaramente visibile nell’immagine a fianco, che mostra un dettaglio del canale R dell’immagine a 8 bit dopo il “maltrattamento” dovuto alla compressione e al conseguente stiramento dei livelli. L’immagine qui è stata naturalmente ri-espansa.
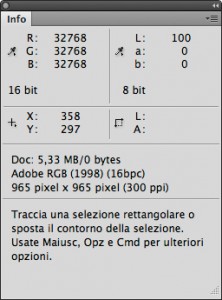
Per parlare di cosa accade sull’immagine a 16 bit dobbiamo innanzitutto specificare che i 16 bit di Photoshop sono in realtà soltanto 15. Come è noto, Photoshop non codifica le immagini a 16 bit in questo formato: i dati dei canali occupano un bit in meno, o quasi (il perché di questo “quasi” si chiarirà tra breve). Questo è facilmente verificabile: create un documento a 16 bit in Photoshop con lo sfondo bianco (255R 255G 255B nella codifica a 8 bit) e impostate la lettura del campionatore principale in modo che vi fornisca i valori a 16 bit. Il colore codificato come bianco si traduce in 32768R 32768G 32768B. Questo accade perché un sistema binario a n bit può esprimere al massimo 2^n stati, dove “^” è l’operatore di elevamento a potenza. Ad esempio, con 8 bit si ottengono 2^8 = 256 stati ed è per questo che i livelli dei canali vengono codificati con numeri che vanno da 0 a 255 (lo 0 aggiunge un’unità, in totale i valori sono quindi 256). Allo stesso modo, con 16 bit si ottengono 2^16 = 65536 stati, e la codifica corretta dei canali dovrebbe avvenire con valori che vanno da 0 a 65535. Photoshop invece arriva a 32768 al massimo. Questa è un’anomalia: ci rivela che la codifica è in realtà a 15 bit (2^15 = 32678), ma il numero più alto dovrebbe essere 32767, ovvero un’unità più basso, in quanto per arrivare a 32678 servono di fatto 16 bit (l’equivalente binario è 1000 0000 0000 0000). La spiegazione è questa: la codifica è di fatto a 16 bit, nel senso che vengono utilizzati tutti e 16 i bit, ma non tutti i 65536 stati sono disponibili e in totale ne vengono utilizzati soltanto 32769. Questo è stato spiegato da Chris Cox, uno dei programmatori Adobe, in questo articolo su un forum ufficiale Adobe.
Comunque sia, ciò che ci importa è quello che accade nella realtà. In un’immagine codificata a 16 bit che venga sottoposta alla compressione dei livelli in output descritta al passo 8 della procedura descritta sopra, il valore 0 viene mappato a 15420, il valore 1 (inteso a 8 bit, non a 16!) viene mappato a 15428, il valore 2 (sempre a 8 bit!) viene mappato a 15436, e via dicendo. La formula simbolica è la seguente: la compressione che abbiamo descritto produce valori secondo questa formula:
Output_16_bit_compresso = 15420 + 8 * Input_8_bit_originale
In teoria, almeno: ci sono in realtà delle discrepanze nella lettura di Photoshop (ad esempio, un valore di 10 come input fornisce un risultato pari a 15501, non 15500 come ci si aspetterebbe), e alla fine il valore 255 viene mappato a 17476 e non 17460 come ci aspetteremmo. Il risultato finale è che ci sono 17476 – 15420 = 2056 livelli nel mezzo e i conti non tornano alla perfezione, perché ce ne aspetteremmo 2040.
Torniamo alla regolazione Livelli. Le caselle in cui digitiamo i valori 120 e 136 ragionano a 8 bit anche quando l’immagine è a 16 bit: possiamo digitare 120, ma non il suo equivalente a 16 bit. Pertanto i 16 livelli totali compresi tra 120 e 136 vanno pensati come livelli a 8 bit. Ma in 16 bit, ognuno di quei livelli ne contiene molti di più, perché la suddivisione numerica è molto più fine. In totale, quindi, ne avremo 16 x 8 = 128. Ma… qualcosa non quadra. Ce ne aspetteremmo 256, se dovessimo accettare che l’immagine non cambia una volta che viene ri-espansa tramite i passaggi 12 e 13 della nostra ricetta, corretto?
Infatti: la procedura descritta all’inizio dell’articolo è formalmente errata. Non tiene conto del fatto che la codifica reale di un’immagine in Photoshop non è a 16 bit reali ma a 15 bit + 1. Se lavorassimo a 16 bit reali tutto tornerebbe, ma i valori corretti per rimappare tutta l’immagine a 16 bit senza perdite dopo la compressione non sono 120 e 136, bensì 112 e 144, in quanto 144 – 112 = 32 livelli. Avendo ogni livello 8 sottolivelli, il numero totale di livelli è pari a 32 x 8 = 256, e pertanto non perderemmo un solo dato nella ri-espansione al massimo del range.
So che tutto questo può sembrare nebuloso, ma portate pazienza perché sto per arrivare alle conclusioni. Devo però darvi un paio di informazioni, prima, e non sono molto rassicuranti.
La prima è che ho barato, biecamente. Tutto il discorso fatto sarebbe ineccepibile se noi avessimo sviluppato un’immagine in ACR a 8 bit e l’avessimo poi convertita in Photoshop a 16 bit. In quel caso saremmo partiti da un’immagine che avrebbe al massimo 256 livelli per canale, e avremmo allargato questi livelli su una griglia molto più ampia. Qualsiasi operazione successiva, in linea di principio, potrebbe essere meno impattante a 16 bit che a 8 bit, ma l’informazione originale non cambierebbe nella pura conversione: un’immagine semplicemente promossa a una profondità di bit superiore non è di per sé migliore dell’originale, perché contiene la stessa quantità di informazione. Quello che io ho fatto, però, è stato sviluppare l’immagine in ACR a 16 bit: e dal momento che un file raw contiene in linea di principio più informazione di quanta ce ne possa stare in 8 bit, ci aspetteremmo che lo sviluppo a 16 bit possa contenere invece più informazione reale di quello a 8 bit.
La seconda è che il nostro esperimento dimostra è che non siamo poi così sensibili alla posterizzazione, perlomeno fino a che non diventa estrema. Il lungo ragionamento effettuato qui sopra, che si conclude con l’affermazione che la procedura è errata, dimostra in buona sostanza che per una svista non stiamo prendendo 256 livelli “spalmati” su 32768, avvicinandoli e poi ri-espandendoli, bensì 256 livelli, e comprimendoli in 128. Ovvero, stiamo di fatto posterizzando la nostra immagine a 128 livelli. Ma non vediamo alcuna differenza a occhio nudo.
Provate per credere. Aprite un’immagine simile a questa e applicate la regolazione Posterizza (Menu Immagine -> Regolazioni -> Posterizza…). Nella casella che vi permette di scegliere i livelli inserite 128 e giocate con l’anteprima. Riuscite a vedere una differenza? Quella che state osservando è un’immagine a 7 bit, a tutti gli effetti. Provate con il valore 64: vedete differenze? Siamo a 6 bit effettivi. Posterizzando a 64 livelli riesco a vedere differenze soltanto nel cielo, in media. Attenzione: un gradiente sintetico soffre subito, perché si spacca in bande, ma un’immagine non è un gradiente e soprattutto non è sintetica; contiene microvariazioni, a volte reali e a volte casuali (rumore) che sono assai meno sensibili alla posterizzazione rispetto a un gradiente. Se scendiamo a 32 livelli la codifica reale della nostra immagine è pari a 5 bit e a questo punto, ovviamente la posterizzazione si inizia a vedere molto chiaramente. Ma sopra questo limite, in molte immagini è praticamente impossibile notarla.
Ciò che questo esperimento dimostra sulla profondità in bit, con il suo errore, è solo che la codifica dell’immagine è assai più larga a 16 bit e che operazioni che potrebbero sembrare distruttive sono in realtà sostanzialmente innocue. Ma non prova nulla, assolutamente nulla, sulla superiorità del contenuto di uno sviluppo di un file raw a 16 bit rispetto a quello ottenuto lavorando a 8 bit. Se prendete il file sviluppato a 8 bit e lo promuovete a 16 bit in Photoshop non inserite alcuna nuova informazione nell’immagine. Applicatelo ora sopra lo sviluppo originale a 16 bit e cambiate il metodo di fusione del livello in Differenza. Con il contagocce impostato su Punto Campione esplorate l’immagine. La massima discrepanza che avrete tra le due immagini è pari a un punto RGB per ciascun canale, leggendo in 8 bit; ovvero, non esiste. Può essere addebitata al dithering, ovvero alla piccola quantità di rumore che viene iniettato nelle immagini quando si riduce il numero di bit per evitare banding ed effetti collaterali, o a qualche particolarità dell’algoritmo di sviluppo, ma non dimostra nulla sulla superiorità di un’immagine rispetto all’altra.
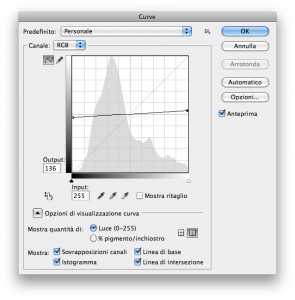
La conclusione definitiva è difficile da trarre perché tutto questo è necessariamente molto image-dependent. Ma la mia impressione è che l’esperimento proposto, sbagliato tra l’altro, serva solo a dimostrare che un’immagine a 16 bit offre più spazio di manovra rispetto a una a 8 bit. Questo può produrre dei miglioramenti quando abbiamo a che fare con manovre così estreme da poter causare posterizzazioni, manovre che abbiano un’entità simile a quella che vedete nell’immagine qui a fianco (si tratta dell’equivalente della compressione dei livelli di output operata prima con la regolazione Livelli), ma in generale non cambierà molto. Se avete a che fare con immagini che vanno stampate in dimensioni enormi, dove ogni minimo artefatto può creare problemi, allora forse i 16 bit hanno un senso. Se avete immagini in cui il colore varia in maniera continua e micrometrica (sto fingendo che non ci sia rumore per inciso), anche qui forse i 16 bit hanno un senso. In tutti gli altri casi, in pratica, a mio parere no.
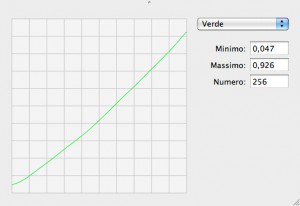
E vi lascio con una provocazione. Qui a sinistra vedete la risposta del verde tratta dalla tabella della scheda video di uno dei miei monitor. Le informazioni sono tratte dal profilo del monitor stesso ottenuto dopo un’accurata calibrazione. Certamente la riconoscete: è una curva che alza il punto d’ombra e abbassa il punto di luce per questi fosfori. I 256 livelli iniziali, se si fanno i conti, vengono mappati in 224 livelli complessivi. 32 livelli non vengono utilizzati: più del 10% del totale. Manca ancora molto per perdere un bit, perché sappiamo che i livelli di un’immagine codificata a 7 bit effettivi sono 128, ma questa curva, come qualsiasi altra, causa… una posterizzazione. Il fatto che la vostra scheda video sia a 8 bit non significa che possiate vedere tutti i valori che è in grado teoricamente di mostrare: le curve dei profili utilizzate per la gestione software del colore posterizzano sempre, poco o tanto – a meno che non siano perfettamente rettilinee e a 45%, e questo non succede mai.
Insomma, è un mondo complicato: e spesso ci preoccupiamo di questioni teoriche che vengono date per scontate, come il fatto che 32769 livelli (li ho contati tutti!) siano sempre migliori di 256. Salvo poi scoprire che ne visualizziamo, in un caso come questo, una buona manciata meno di 256.
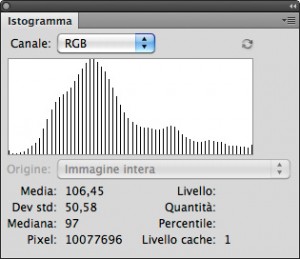
Pertanto, attenzione agli esperimenti che non abbiano una precisa e solida base scientifica, e soprattutto alle affermazioni relative al fatto che un istogramma leggermente a pettine sia indice di malattia terminale. Quello riportato qui a fianco, ovviamente lo è, vero? C’è un valore ogni quattro, quindi figuriamoci: l’immagine da cui è tratto dev’essere atroce e inguardabile, no? Giudicate voi. Qui sotto riporto l’immagine originale e quella che genera quest’istogramma, affiancate: sì, è un dettaglio della fotografia utilizzata in questo articolo, e potete cliccarci sopra per vederlo ingrandito. La parte a sinistra è l’originale, quella a destra è la sua posterizzazione a 64 livelli: solo un valore ogni 4 viene preservato, quelli che lo circondano vengono “impaccati” con esso.

Cercate pure le differenze, e se le vedete a occhio nudo e le considerate in qualsiasi modo significative per l’utilizzo dell’immagine, visualizzata a monitor o stampata che essa sia, sapete dove trovarmi… 😉
A presto!
MO



Marco,
Ottimo articolo, complimenti!
Non sai quanto mi scocci fare il calibrazionista della situazione 😉
“le curve dei profili utilizzate per la gestione software del colore posterizzano sempre, poco o tanto – a meno che non siano perfettamente rettilinee e a 45%, e questo non succede mai.”
Probabilmente parlando di “gestione software” hai sottinteso l’eccezione, ma per chiarezza nei confronti dei meno esperti la esplicitiamo: tutti i monitor a calibrazione hardware (Quatographic, NEC Spectraview, ecc ecc) producono profili con rette a 45 gradi – proprio a causa del fatto che è l’elettronica interna che calibra il device (con precisioni che per i Quato ad esempio vanno dai 12 ai 16 bit per canale), e non l’ICC che compensa – a meno che qualcosa vada storto.
Argomento che è un tipico cavallo di battaglia di chi ti vuole vendere un monitor a calibrazione hardware… ed io posso dirlo perché non li vendo più da anni 😉
Davide
Grazie della precisazione, Davide, intendevo esattamente quello che hai scritto ma non volevo allungare troppo un discorso che in fondo era marginale rispetto all’argomento principale dell’articolo. Però la specifica sta benissimo nei commenti :)…
Molto interessante anche se parecchie parti mi sfuggono. Me lo devo rileggere con calma e più di una volta. Son stupido e lento =P
P.s.
Avere un profilo che ha una retta a 45° significa avere una risposta lineare, giusto?
In senso stretto è un sottocaso di risposta lineare. In termini matematici, se hai una quantità y dipendente da x (chiamale output e input, se vuoi), la retta a 45° corrisponde a y = x e questa è certamente una relazione lineare. Ma anche y = x / 2 è lineare, pur non essendo una retta a 45°. Un problema, però, è che noi lavoriamo con numeri interi a causa della quantizzazione del digitale; se x e y fossero variabili continue non ci sarebbero problemi, ma nel nostro campo succede questo: se pensi di avere x = 50 (valore di esempio) y = 50 / 2 = 25. Se ora poni x = 51, nel continuo avresti y = 51 / 2 = 25.5, ma questo non è permesso in un sistema quantizzato. L’approssimazione canonica porta questo valore a 26 (intero superiore, perché la parte decimale è maggiore o uguale a .5). Fin qui, di nuovo, nessun grosso problema. Salvo che… per x = 52 hai y = 52 / 2 = 26. Quindi hai *due* valori distinti di x (input) che corrispondono a due valori identici di y (output). Come comprendi questo fa cadere in senso stretto il concetto di linearità, perché la funzione che lega y a x non è più, come si dice in termini tecnici, iniettiva. In poche parole, a elementi distinti del dominio (x) non corrispondono sempre elementi distinti del codominio (y).
Le ricadute principali di questo fatto sono due. La prima è che quella che noi vediamo come una retta è in realtà una scalinata che ci appare come lineare perchè gli scalini sono tanti e noi li guardiamo da una certa distanza. La seconda è che qualsiasi curva posterizza in qualche misura l’immagine. Come faccio vedere nell’articolo questo non deve farci strappare i capelli semplicemente perché non ci accorgiamo di certe posterizzazioni, che sono davvero minime. Se le cose vengono portate all’estremo, naturalmente abbiamo un problema serio. La soluzione a quel punto è portare la fotografia in Illustrator e darci alla fumettistica. 🙂
Decisamente più chiaro 😀
Ultima domanda ^^”” e perdonami se utilizzo termini non propriamente tecnici
Nel caso di un file raw, nello sviluppo dello stesso, ci sono determinate proprietà (tipo l’esposizione) che sfruttano la linearità dei dati del raw stesso (linearità del tipo x=y ?)
Nel momento in cui terminiamo lo sviluppo e lo apriamo in un qualsiasi programma di editing fotografico, perdiamo questà linearità dei dati giusto?
E tutto questo a “causa” di alcuni fattori come l’applicazione di una curva tonale?
I dati del raw sono “lineari” (virgolette obbligatorie) nella misura in cui rappresentano i valori catturati dal sensore senza manipolazione. Naturalmente i valori di luminanza vengono tradotti in tensioni elettriche, quindi un qualche tipo di conversione fisica esiste, ma tolta questa la rappresentazione è fedele. Alcune delle proprietà come l’esposizione si basano sul fatto che la profondità in bit del segnale catturato è maggiore di quella che viene salvata in un file jpeg a 8 bit; di norma si tratta di 12 o 14 bit, e a quanto ne so certi sensori arrivano a 16. Quanto poi questi bit siano del tutto significativi (possono essere viziati da rumore e altri problemi) è tutto da verificare.
La linearità come tu la intendi si perde nel momento in cui il file raw viene trasformato in raster. Il gamma dei profili RGB più diffusi è di 1.8 o 2.2. Se vuoi qualche informazione in più su questo complicato argomento (che è connesso a un sacco di fattori, tra i quali la nostra percezione della luminanza e le curve di risposta dei monitor) forse puoi trovare qualche spunto qui (solo in inglese).
Ottimo, ottimo articolo!
Grazie mille, Stefano!